1.対角線が直径である四角形の向かい合う角の場合

これから直径を使った円に内接する四角形の書き方を説明します。
内接する四角形の描き方
- 最初に円を描きます。
- 直径を通る直線を引きます。
- 直径を底辺とする△ABCと△ABDを円に内接するように描きます。


つぎはなぜ四角形の対角が合わせて180°になるかを説明します。
対角が合わせて180°になる理由(対角線が直径を通る場合)
直径ABに対する円周角(弧ABの円周角)は∠ACB=90°です。同様に直径ABに対する円周角(弧ABの円周角)は∠ADB=90°です。 よって向かい合う角度は90°+90°=180°となります。
2.対角線が直径とならない四角形の向かい合う角の場合
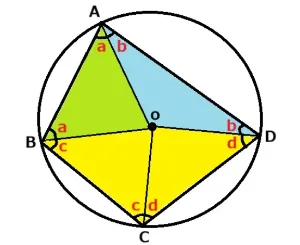

さらに四角形の対角線が直径を通らなくてもなぜ対角が合わせて180°になるかを説明します。
対角が合わせて180°になる理由(対角線が直径を通らない場合)
上図でわかりますようにOを頂点とした4つの二等辺三角形の底角はaa、bb、cc、ddで成り立っています。よって四角形ABCDは360°で2×(a+b+c+d)で構成されています。
内接する四角形の向かい合う角はご覧のようにa+b+c+dで成り立っているので半分の180°です。どちらの対角もa+b+c+dになっていますね。
3.三角形AEDと相似な三角形を見つけましょう
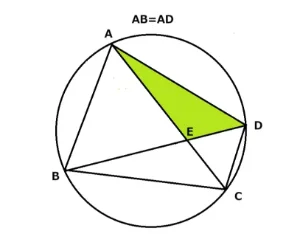

円の中にできた三角形AEDと相似な三角形の見つけ方を説明します。図の中に〇✖を書き込んで相似の三角形を見つける方法なので見つけるのが簡単です。
〇✖を使って相似な三角形を見つける
まず、△ABDはAB=ADの二等辺三角形です。よって∠ABD=∠ADBになります。下図の〇で示しました。続いて弧ABの円周角が∠ACB=∠ADBとなり,また弧ADの円周角∠ABD=∠ACDも〇で示しました。
さらに弧CDの円周角∠CBD=∠DACは✖で示しました。

上図により△AEDは二角が〇✖で示されているので同じ〇✖の三角形を探せば相似の三角形が見つけられます。したがって△ADCと△BECがそうです。
答え △AED∽△ADC、△AED∽△BECの二組です
4.練習問題

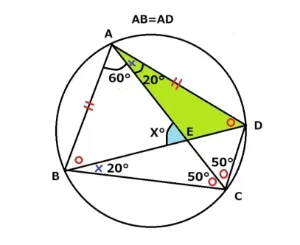
三角形ABDは二等辺三角形です。また∠BAE=60°、∠EAD=20°のとき∠AEBを求めましょう。


∠BADの対角から攻めていく方法を解説します。
まず初めに∠BADに着目すると80°です。内接する四角形の対角は合わせて180°なので80°を引くと∠BCD=100°となります。
AB=ADなので弧AB対する円周角∠ACBと弧AD対する円周角∠ACDは等しいです。〇〇=100°なので〇=50°つまり∠ACB=50°です。また弧CDの円周角により∠DAC=∠CBD=20°です。これらからX°は〇+✖の外角ですので50°+20°=70°となります。
答え 70°

もう一つのアプローチもあります。このアプローチは対角に気づく前に円周角から攻めたやり方です。最初の着目点は少し違いますが最終的には三角形の外角を使って求めています。
まず△ABDは二等辺三角形なので底角は∠ABD=∠ADBとなります。これら2つで100°なので1つの底角は50°です。
つぎに弧ABの円周角∠ADB=∠ACBへと目を移しますとやはり50°であることがわかります。これでX°は〇+✖の外角ですので50°+20°=70°となります。
5.まとめ

今回の円の問題に関することをまとめてみました。問題を解いた後でまとめを読んでみてください。さらに成果が上がりますよ。
- 円に内接する四角形の向かい合う対角は合わせて180°になります。
- 円の中に中心Oがあるときは各頂点に線を引き二等辺三角形を作ってみましょう。
- 相似な三角形を見つけるときは〇✖を使ってみましょう。それぞれの三角形で二角を見つければ相似となります。
- 三角形の外角を常に意識しましょう。