y=ax+bのbがあるだけで一次関数は難しいと思い込んでいませんか?実は日常生活の中のことを式に表してみると「なるほどね。」と実感できます。では身近なことを挙げてみましょう。
例えばお買い物、電気料金そして所持金から毎月の一定のローンを差し引くことなどが式に表せます。
実際にどのようなことなのか y=ax、y=ax+b、y=-ax+bで検討していきましょう。
クリックできる目次
1.同じものを購入した時の個数と金額を表したy=ax

1個120円のアイスクリームを2個3個と購入しました。これをグラフで表すと次のようになります。
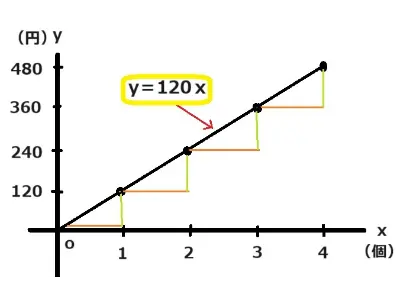

個数が2倍、3倍とふえると金額はどうなりますか。

金額も240円、360円と2倍3倍となっていますね。

これが正比例ですね。正比例も1次関数です。また個数が1個増えるごとに値段は120円ずつ増えていますね。つまり、a(傾き)=120となります。そしてこのグラフが0から出発しているのは当たり前のことですが、購入しなければ0円だからです。したがいましてこの式はy=120xとなります。
2.基本料金がある場合はy=ax+bで表す

電気料金について見ていきましょう。(段階料金は考えないものとします。)例えば1kwごとに30円の料金がかかり基本料金は2000円だとします。これをグラフで表してみます。
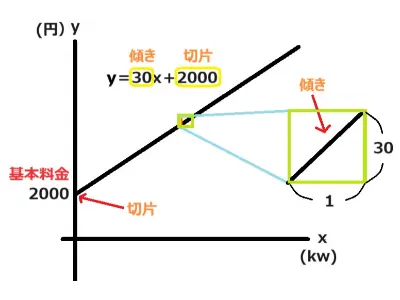

傾きや切片はどうなっていますか。

1kwごとに30円ずつ増加していますのでa(傾き)=30になります。電気料金は電力を使用していなくても契約料として基本料金がかかります。だから基本料金つまり切片が2000から始まっているのだと思います。

その通りですね。電力を使用していなくてもお金がかかるのです。それが切片で表されているのです。よって式はy=30x+2000になります。

では次の問題を考えてみましょう。
今月の料金を3500円以下に抑えたいと思います。電力使用を何kwまでにすれば良いでしょうか。
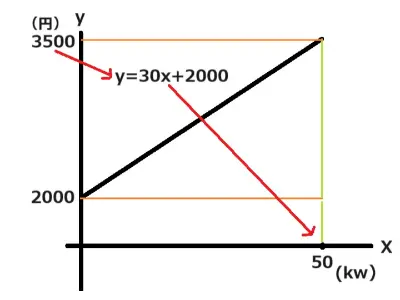

y=30x+2000の式の合計金額はyのことですのでyに3500円を代入します。これを計算しますとx=50となりますので50kw以下に抑えれば良いことがわかりました。 答え 50kwまで

よくできました。合計金額3500円はyで表されているのでyに3500を代入するところがみそですね。
3.ある金額から一定の金額が減っていく場合を表すy=-ax+b

ある人の所持金54万円から毎月のローン6万円が引かれます。これを式で表すとどうなりますか。

所持金は54万円から6万円ずつ減っていきますよね。この減っていく様子がy=-ax+bで表されます。最初に54万円ありそこから6万円ずつ減っていくのでy=54-6xになります。
答え y=-6x+54


よくできました。減っていく様子を表す式はy=-ax+bですね。
では上記の問題のつづきを考えてみましょう。
何か月で所持金はなくなるでしょうか。
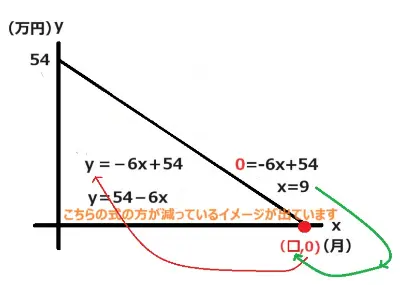

所持金はyで表されていますのでy=-6x+54のyに0を代入します。xは月数です。これを解きますとx=9となりますので9か月で所持金がなくなります。 答え 9か月

よくできました。最初にyを所持金、xを月数と把握しておくことが大切です。
4.二人の所持金が等しくなる月数の問題は連立方程式を使う

Aさんは毎月3万円ずつ貯金をします。手元のお金はありません。Bさんは所持金91万円から毎月のローン4万円が引かれます。二人の金額が等しくなるのは何か月後ですか。
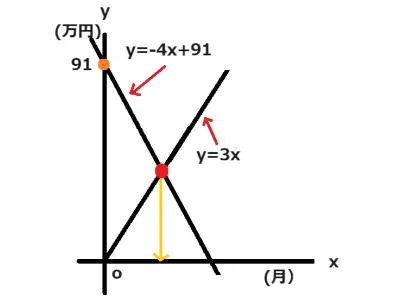

初めに2つの式を作ってください。

はい、Aさんは0円から出発して毎月3万円ずつ増えていきますのでy=3xで表せます。Bさんは所持金91万円から毎月4万円ずつ減っていくのでy=-4x+91(イメージとしてはy=91-4xが理解しやすいです。)と表せます。

それからどうしますか。

グラフの交点は二人の所持金が同じでその月数がわかります。よって連立方程式で交点の座標のxを求めます。y=3xの3xをもう一方の式に代入します。
すると3x=-4x+91になるのでこれを解くとx=13になります。 答え 13か月後
ちなみに二人の所持金はどちらかの式にx=13を代入しますと39万円とでます。
5.まとめ
日常生活の出来事を式にしてみました。実生活のことを式で表した方が具体的でわかりやすかったでしょうか。
特に切片があるときは基本料金(使用してもしなくてもお金がかかる。)などと考えてほしいと思います。
その他プールに一定の水があってそこから水を入れていく場合も一定の水は切片になります。またアイスクリームみたいに購入しなければ0円なので切片はありません。
これらの区別がはっきりすれば一次関数の基礎を理解したことになります。