受験生にとって算数、数学はどなたもすぐに得点や偏差値アップを狙いたいですよね。そんな方がたのために問題の難易度のとらえ方やそれによる偏差値アップの方法を提案しました。
1.入試問題はどのような考え方で作られているのか
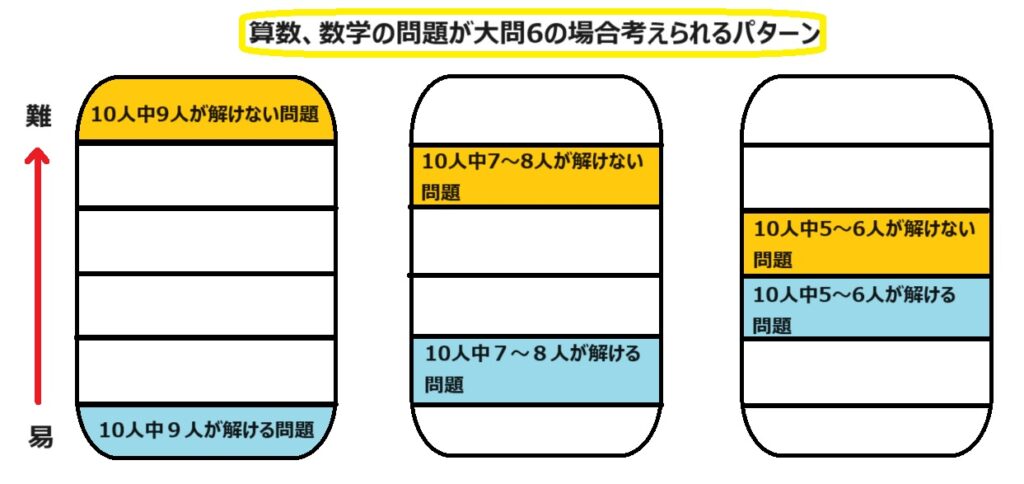
このようにして作ることで算数、数学の平均点が50点前後になるように作られていると勝手に推測しています。
簡単な問題ばかりだと受験生の皆さんが高得点をとってしまうので合否判定は難しいです。
逆に難問ばかりだとどなたも得点できませんのでこれまた厄介です。
そこで自分なりに図のような結論に至りました。
2.まずどの問題から克服するべきか
先ずは図で示しましたように自分の実力に合わせた段階の問題選びです。
例えば、50点以下の方であれば10人中5~6人が解ける問題までをトライしましょう。図は大問6を想定していますので3番までは解けるかどうかです。
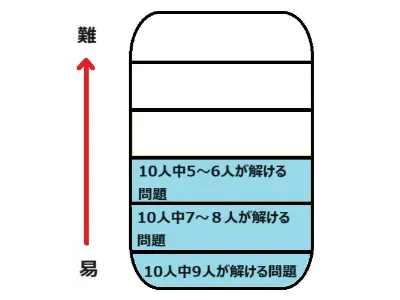
つぎに70~80点くらいの方は10人中7~8人が解けない問題まで挑戦しましょう。
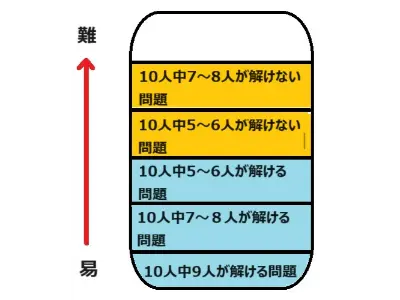
最後に80~90点の方は最難問に挑戦です。この方たちの実力レベルを目に見えて上昇させるのは難しいです。扱う問題が高難度なので地道な努力が必要です。それと同時にどの単元が自分にとって難しいのかを知る必要があります。
これはあくまで大問6のパターンです。もし自分の受験する高校が大問8まであればこの図を参考にして作り変えてみてください。そうするとより一層わかり易くなると思います。
3.どんな難易度の問題であるかを見極める力をつける
中3実力テストの場合
8月までは中1~中2の復習と3年生1学期までの復習問題になりますが入試問題と同じように後半の方が難易度は高いです。
9月以降の実力問題は入試問題に照らし合わせて作られる本格問題なので同じ単元の問題でもレベルアップした問題となりますので後半の問題を特に吟味しましょう。
入試問題の場合
公立高校であれば都道府県立過去問1冊あれば十分検討できますが、私立高校は学校によって傾向が変わってきますし難易度もそれぞれです。
これらの問題を検討していくうちに、例えば平面図形なのか立体図形なのか、順列組み合わせなのか、規則性の問題なのかなど、どの単元がこれから対策すべき問題なのか明確になってきます。
こうして比較検討しながら学習していきますと流行りの問題がわかってきますので早めに取り組んだ方が良いと思います。
結論
どの問題が1番難しいかの見極めは素直に考えて最後の問題です。人によって得意不得意を考慮しても最後の2問です。
なぜなら、途中で1番難しい問題を出してしまって残りの問題まで手を付けられなかった、そして時間さえあれば残りの問題も少しはできたのにという声が出てくるようでは問題作成が失敗の可能性を指摘されかねません。これはあくまでも公立高校問題の場合です。
しかし、私立は違います。独自の方針に基づいて作られていますのでその点は自由です。問題も甲乙つけがたいし、順番も計算問題以外はランダムかもしれません。
4.まとめ
入試問題の作られ方を意識されると自分はどの単元のどのレベルの問題を克服していけば良いのか、これからの方針が立つと思います。
自分にとって無謀と思われるような高難易度問題から出発しないで一歩一歩段を上るように自分にとって難易度が合う問題から上を目指して解決していくのが偏差値アップの秘訣です。