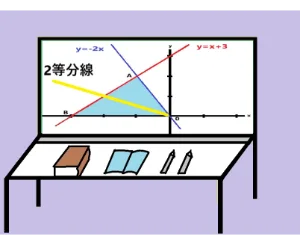
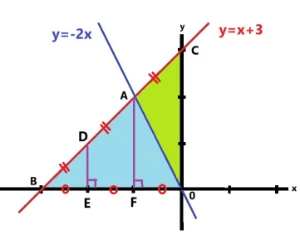
*今回は点A、点B、点Oのそれぞれの点を通って三角形を2等分する式を3つ求めたいと思います。
クリックできる目次
1.2直線の交点を求める

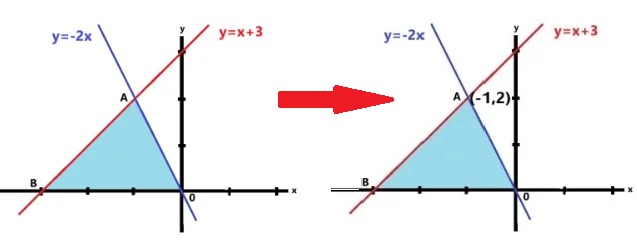
これから面積を2等分する直線の式を順を追って説明したいと思います。まず初めは2直線の交点Aを求めます。
y=x+3とy=-2xの交点を求めるにはこれら2つの式の連立方程式を解きます。代入法で解きますと最初の式はx+3=-2xとなります。これを解きますとx=-1、y=2になります。
2.中点の求め方

つぎは三角形ABOの面積を点Aを通って2等分する方法です。まず辺BOの中点を求めます。この問題では図からすぐにわかりますが中点が分数のときもありますので公式を覚えましょう。
中点を求める公式
2点(X,Y)(X´,Y´)の座標がある場合:X座標は(X+X´)÷2で求めることができます。Y座標は(Y+Y´)÷2で求められます。

では公式を使って辺BOの中点を求めてみましょう。点Bの座標は(-3,0)でげんてんOは(0,0)です。X座標は(-3+0)÷2=‐3/2です。Y標は(0+0)÷2=0ですので中点は(-3/2,0)と決まりました。これを点Cとします。
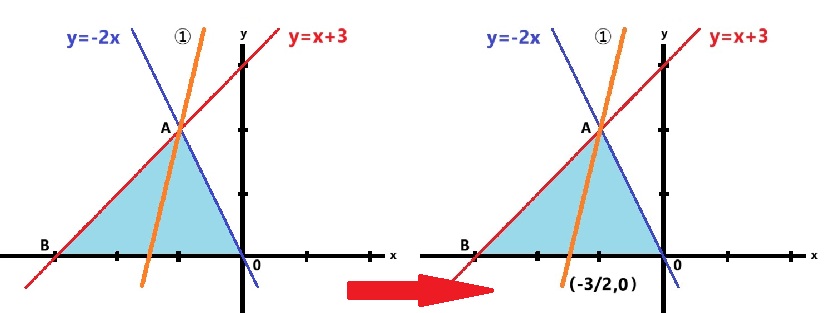
3.2点の座標から直線の式を求める①

点A(-1,2)、点C(-3/2,0)の2点からy=ax+bに各座標をあてはめて連立方程式で解きましょう。
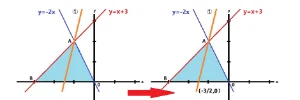
連立方程式でACを通る直線の式を求める
まずy=ax+bの式に点A(-1,2)を代入すると2=-a+bとなります。つぎにy=ax+bの式に点C(-3/2,0)を代入すると0=-3/2a+bとなります。この2つの式を連立方程式で解きますとa=4,b=6です。ゆえに三角形ABOを2等分する直線はy=4x+6になりました。 答え y=4x+6
4.2点の座標から直線の式を求める➁

つぎは三角形ABOを2等分する直線は原点Oを通る直線です。初めに点A(-1,2)と点B(-3,0)の中点を求めましょう。公式よりx座標は{-1+(-3)}÷2=-2、y座標は(2+0)÷2=1よって中点の座標は(-2,1)となります。この点をDとします。

正比例の式で直線DOの式を求める
点D(-2,1)をy=axにあてはめてください。原点Oを通っているので切片である+bは必要ありません。すると1=-2a、つまり-2a=1なのでa=-1/2となりました。よって直線DOの式はy=-1/2xです。答え y=-1/2x
5.2点の座標から直線の式を求める③

おしまいの2等分線は辺AOの真ん中を通る直線です。点Aの座標は(-1,2)、点Oの座標は(0,0)なので公式よりx座標は(-1+0)÷2=-1/2、y座標は(2+0)÷2=1よって中点の座標は(-1/2,1)です。この点をEとします。

連立方程式でBEを通る直線の式を求める
まずy=ax+bの式に点B(-3,0)を代入すると0=-3a+bとなります。つぎにy=ax+bの式に点E(-1/2,1)を代入すると1=-1/2a+bとなります。この2つの式を連立方程式で解きますとa=2/5、b=6/5です。ゆえに三角形ABOを2等分する直線はy=2/5x+6/5になりました。答え y=2/5x+6/5
6.三角形ABOと三角形AOCの面積比

△ABOと△AOCの面積を比べてみましょう。最初の方法は通常の底辺×高さ÷2を使います。つぎは相似比を使った方法で求めてみます。
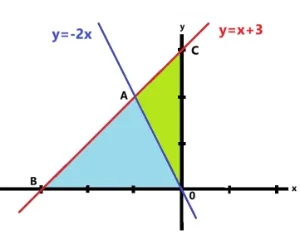
それそれの面積を出して求める
△ABOは底辺が3高さが2なので3×2÷2=3、△AOCは底辺が3高さが1なので3×1÷2=3/2です。比にしてみますと3:3/2=6:3=2:1となりました。 答え 2:1
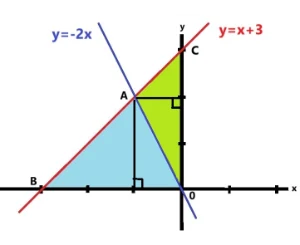
相似比を使って面積を考える
△CBOをy軸と平行に直線DEと直線AF引いてみました。すると辺CBはCA、AD、DBと3等分されました。もちろん辺BOもBE、EF、FOと3等分されています。つぎは三角形を左に回転させ△OCBになるようにします。
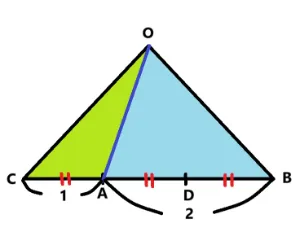
△OCBを見てください。辺AB:辺CA=2 : 1に分かれています。これらの三角形は相似ではなく高さが同じ三角形なので底辺の比が面積比になります。 答え 2:1