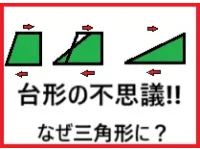
今回は台形がいかにして三角形に変化していくのかを図と面積の公式で考えてみました。
また平行四辺形も三角形2つから面積の公式を導きました。
このような変化がおもしろいと思えるお子様はどんどん図形や面積が好きになるでしょう。図形でお困りのご父兄は以下の指導法をご覧ください。(4、5、6年生対象)
1.台形が三角形になる

これから台形がなぜ三角形になるのかを二つの面から検討していきましょう。

台形は四角形だから三角形にはなりません。どうしてですか。

まず図で説明します。次のようになります。
上底を縮めた⇒上底を縮めた分だけ下底を伸ばす⇒上底が完全になくなった⇒上底が下底に足され三角形になった
つまり、形は変化したが面積は同じなので台形は変形すると三角形なのです。
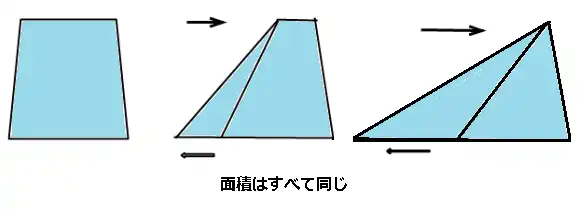

二つ目は台形の面積の公式からの説明します。
台形の面積は(上底+下底)×高さ÷2です。
(上底+下底)の上底がなくなりその分の長さが下底に加わり底辺となる
(上底が0に+下底)=もとの底辺にプラス上底=長くなった底辺
*三角形の面積は底辺×高さ÷2です。よって(上底+下底)=底辺なので台形面積は三角形と同じ公式になります。
台形の面積=三角形の面積
台形は三角形に変化できると解釈できます。
②を丁寧に何度もお子様に教えてください。
またその際にはフリーハンドでOKですから必ず図形を書かせて特徴を言えるようにさせてください。
ただし定規の使い方とコンパスの使い方はノートに正確にやらせてください。そして図形は面白いと伝えましょう。
お母さんとサラちゃんの会話例

台形の形は文字通り台の形だからイメージしやすいけど面積の公式については何か変な感じがするでしょ。

(上底+下底)の部分が理解しにくいです。

四角形ならば縦×横で済むはずなのにね。

なぜ済まないのですか。

それは上底と下底の長さが違うからよ。

ではどう考えればいいですか。

台形の上底と下底の長さを少しずつ変えていくと分かりますよ。上底を短くしていき、その分だけ下底を長くします。上底+下底の長さは変わりませんね。
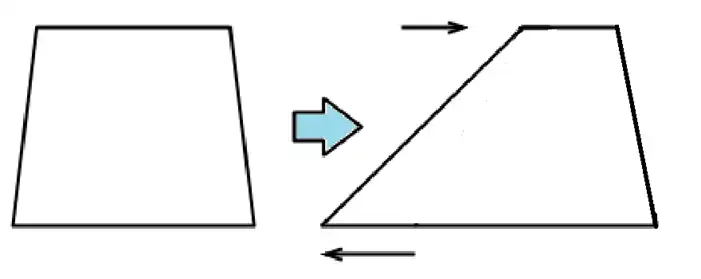

なんかすごく変わったように見えます。

まだよ。これでどうかしら。上底がなくなりその分下底が増えました。
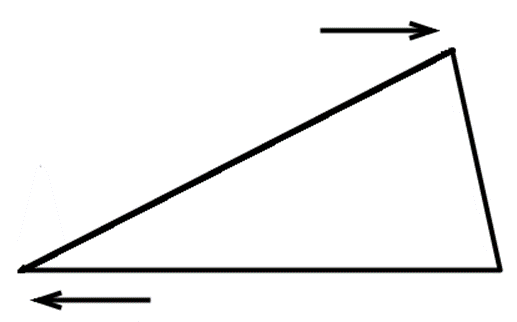

びっくりです。三角形に変身ですね!

でもね、上底の長さが下に移動しただけなの。それで底辺になったので上底+下底=底辺ということです。

お母さん、相変わらずすごいです。

どういたしまして。同じ面積で台形が三角形に変身できる方法をもうひとつ説明します。
- 下底を上底の分だけ延長します。
- 上底の右端から下底の左端に直線を引くと2つ同じ大きさで形も同じ三角形ができました。これを合同な三角形といいます。(2つの三角形がぴったり重なること)
- 上の三角形が下に移動しました。なので上の三角形を消します。
- すると台形の面積を変えないで三角形に変えることができました。
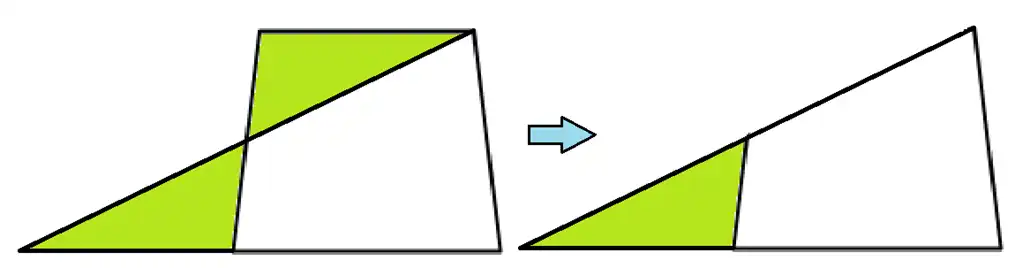

それでは確認のために台形の面積や高さを求める練習をしましょう。解答はまとめにあります。
- 上底が5cmで下底が7cm、高さが12cmの台形の面積
- 上底が8cmで下底が12cm、高さが10cmの台形の面積
- 上底が8cmで下底が12cm、高さがXで面積が180㎠の台形、この高さXを求めましょう。
2. 平行四辺形の定義と性質

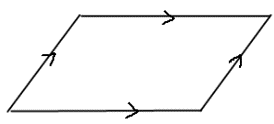
こんどは平行四辺形の定義と性質について検討しましょう。どんな性質があるか言える人はいますか。

はい、2組の向かい合った平行(どこまで行っても交わらない)な四角形です。図は下にあります。

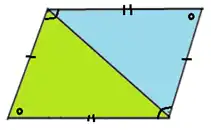
はい、向かい合った角の大きさは等しく、向かい合った辺の長さも等しいです。図は次のようになります。

はい、斜めに傾いた辺をまっすぐに戻すと正方形や長方形になります。つまり、長方形や正方形は平行四辺形の仲間と考えられます。

みなさん、よくできました。
3.平行四辺形の描き方

続いて平行四辺形の描き方です。だれか説明できますか。

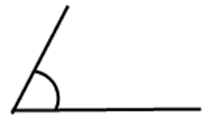
はい、ぼくが説明をします。例えば1辺が2cmと3cm,60°の場合です。
まず3cmの直線直線を引きます。


次に左端に分度器の中心をあてて60°を測り、2cmの直線を引きます。

続いて2つの直線の先スの針を刺し、2cmと3cmを測り交差させます。


最後に交差した所に2つの直線を引けば完成です。
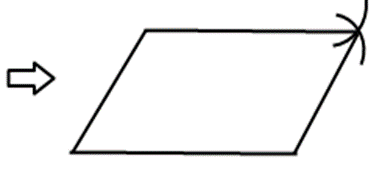

その通りです。よく説明できました。
4. 平行四辺形は三角形が2つある

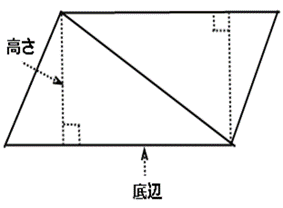
平行四辺形に1つの対角線を引いてみましょう。すると合同な反対向きの三角形が2つできます。ここから平行四辺形の面積について考えてみたいと思います。下の図と説明を見てください。
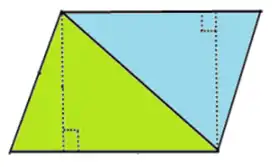
三角形の面積は底辺×高さ÷2です。平行四辺形は三角形2つでできているので、面積は底辺×高さ÷2×2になります。
よって÷2×2は相殺されるので平行四辺形の面積は底辺×高さで求められます。
5. まとめ
面積を変えずに台形が三角形になったり、平行四辺形が対角線1本で合同な三角形2つに分けられ面積についても考察できました。
このように図形の変化を楽しめたなら幸いです。また平行四辺形の中で4辺が等しい場合はひし形でもあります。
*台形の面積や高さを求める練習の解答
- (5+7)×12÷2=72 72㎠
- (8+12)×10÷2=100 100㎠
- (8+12)×X÷2=180 20×X=360 X=360÷20 X=18 18cm