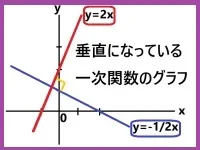
2つの直線がどんなときに垂直に交わるか考えたことがありますか。今回はこれをメインテーマとして扱いたいと思います。
クリックできる目次
1.y=xとy=-xのグラフの関係性
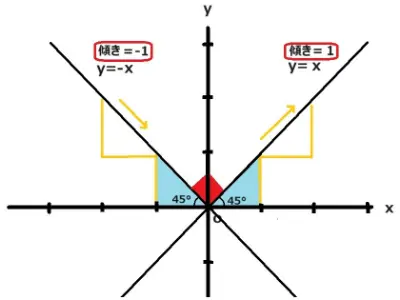

2直線y=xとy=-xがあります。これらの直線が垂直に交わるか検討してみましょう。
解説
y=xは右に1進んで1上がるグラフなのでブルーで囲まれた三角形は直角二等辺三角形です。したがって45°、45°、90°の三角形です。
一方y=-xのグラフは右に1進み1下がるグラフなのでブルーで囲まれた三角形は先ほどと同様に45°、45°、90°の三角形です。
よって2直線に挟まれた角(赤い部分)は90°になります。
2.y=1/2xとy=-2xの関係性
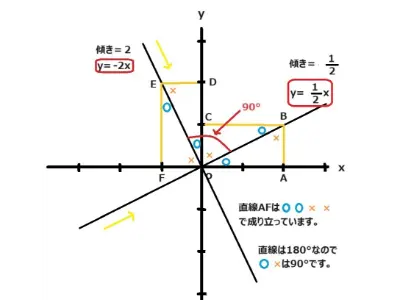

2直線y=1/2xとy=-2xがあります。これらの直線も垂直で交わるか検討していきましょう。
解説
y=1/2xは右に2進み上に1上がる直線です。一方y=-2xは右に1進み2下がる直線です。そしてAからBに直線を引き、続いてBからCにひいてみました。
すると、△ABOと△COBの2つの三角形が作られました。これら二つの三角形は同じ(合同)です。そのあと同じ角度に〇×を付けてみました。
今度は∠AOCに注目します。∠AOCは90°です。この角度は〇×で構成されています。
次にEからD、EからFに直線を引くと△EDOと△OFEの2つの三角形が作られました。これら2つも△ABOと△COBと同じ(合同)です。
続いて∠DOFに注目します。∠DOFは90°です。この角度も〇×で構成されています。すると180°は〇×〇×で構成されていることがわかります。
よって∠BOEは〇×で構成されていますので90°になります。
3.y=1/3xとy=-3xの関係性
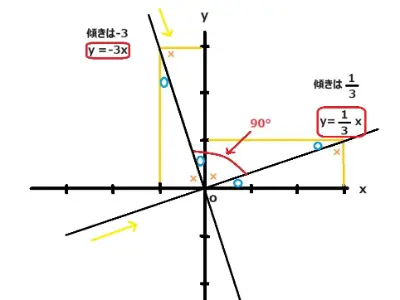

2直線y=1/3xとy=-3xがあります。これらの直線も垂直で交わるか検討していきましょう。
解説
2直線y=1/2xとy=-2xのときと同様に4つの三角形は同じ(合同)です。
2と同様に考えていくと2直線に挟まれた角度は〇×で構成されています。よって90°になります。
4.どんなときに一次関数が垂直になるのか

では2直線はどんなときに垂直になるかその関係を探ってみましょう。
- 1の2直線の傾きは1と-1です。
- 2の直線の傾きは1/2と-2です。
- 3の直線の傾きは1/3と-3です
これら3組の傾きをそれぞれかけ算してみましょう。
- 1×(-1)=-1
- 1/2×(-2)=-1
- 1/3×(-3)=-1
3組とも-1になりました。つまり2直線の傾きをかけ算すると-1になる場合が2直線が垂直になるときです。

わかりました。2直線の傾きを掛けて常に-1になれば2直線は垂直になるのですね。
5.2直線を垂直したいときどんな考え方をすればよいか

それでは直線の式を求めてみましょう。
傾きが4で切片が2の直線と(0,2)を通り垂直になるもう一方の直線の式を求めなさい。
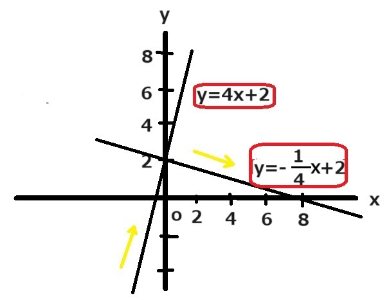

最初の式はy=4x+2でもう一つの式の傾きを-1/4すればかけ算して-1になりますね。もう一つの傾きの求め方は-1÷4です。そして(0,2)を通るので切片は2ですね。よってもう一つの式はy=-1/4x+2となります。
答え y=-1/4x+2

次の問題です。
傾きが3で切片が2のグラフがあります。この直線と(0,2)で垂直に交わるときのもう一方の直線の式を求めなさい。またx軸との交点の座標を求めなさい。
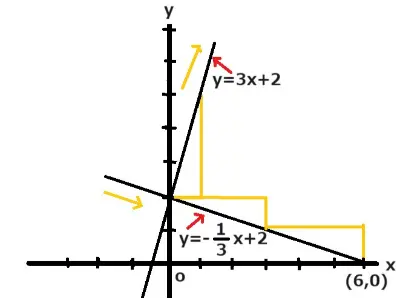

最初の式はy=3x+2でもう一つの式の傾きを-1/3にすればかけ算して-1になりますね。求め方は-1÷3です。
そして(0,2)を通るのでもう一つの式はy=-1/3x+2となります。
またx軸との交点は(□,O)でy座標は0なのでy=-1/3x+2の式にy=0代入します。すると0=-1/3x+2になりますのでx=6になります。よってx軸の座標は(6,0)になります。
答え y=-1/3x+2、(6,0)
6.まとめ
*2つの直線が垂直に交わるときの公式
傾き×傾き=-1でどちらか一方を求めるときは-1÷傾きです。今回の公式をしっかり復習してください。