割合は小3から小4にかけて学習した分数、小数を本格的に数字で表したものです。
それは単なる数字だけでなく%(パーセント)や割、歩、厘といった歩合でわかりやすく表現しています。
ところが割合をどう理解すればよいのか最初のイメージをつかむのが難しいと思います。
そこで最初に円グラフ、棒グラフ、帯グラフでイメージをつかみやすく工夫してみました。
さらにはイメージから公式へ導き、問題演習が楽になるようにしました。
最後にはイメージ⇒公式⇒問題演習と順序だてるとほかの単元においてもかなり役に立つのではないでしょうか。
お子様が割合の表をマスターする際にはご父兄のお手伝いが必要になることがあるかもしれませんが、そのときはご協力をお願いします。
クリックできる目次
1.割合のイメージをつかむ

割合を示すグラフ(黄色を中心に考えた場合)を3つ図に示しました。黄色い部分の割合は黄色÷全体です。一般的には目盛りなどが付いていてよく%で表されていますが、数字が無くても見た目で割合が大きいか小さいかはわかりますね。この図を繰り返し見ることでイメージがつかめたら、つぎは公式を覚えていきましょう。
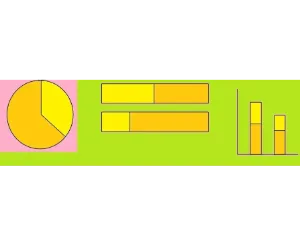
2.割合の公式をグラフでつかむ

まず、最初は図で割合をみていきましょう。どのグラフも黄色(比べられる量)÷全体(もとになる量)で求めます。この図を上から順に3パターン繰り返し見ることでイメージがつかめます。つぎは言葉でも公式を覚えていきましょう。
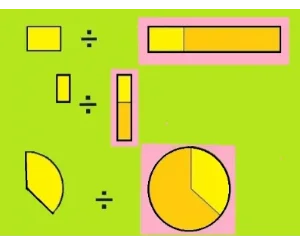
3.割合の公式を言葉で覚える

割合の公式は比べられる量÷もとになる量と覚えます。言葉のほうが少し難しく感じてしまいますね。そしてこの公式を入れ替えてみます。するとつぎのように変えられます。これも覚えましょう。
- 比べられる量はもとになる量×割合
- もとになる量は比べられる量÷割合
4.連比を使ってデータを比較してみよう

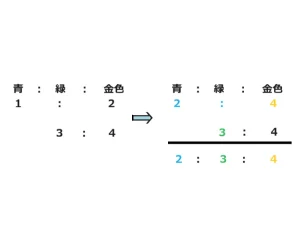
連比とは3つ以上のデータを正しく比較するために使います。例:青と緑と金色で考えてみましょう。
青:金色=1:2、緑:金色=3:4となっています。単純に数字だけを見て青:緑=1:3というわけにはいきません。
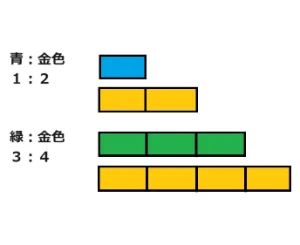

もとになる金色の数字が2と4になっていますね。この数字が違っていては青と緑が比べられません。ではどうすれば良いでしょうか。金色の数をそろえてあげると青と緑が比べられます。青:金色が1:2ですからそれぞれを2倍して2:4にしてはじめて比較ができますね。それが下の図です。金色が4になったことでそれぞれの数字を見ますと青=2、緑=3、 金色=4となっています。
よって青:緑:金色=2:3:4となります。
5. 円グラフの異なるスケールのデータ比較

円グラフでA国とB国の鉄鉱石の輸出量を比べてみましょう。2国の輸出量を比べるとき円グラフだけを見るとA国の65%、B国の30%で明らかにA国が多いです。
しかし、ベースとなる量がそれそれ違いますので計算をしなければ違いがはっきりしません。
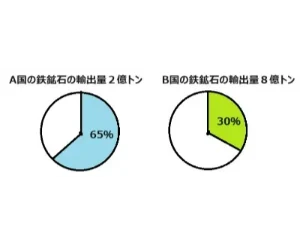
A国の場合:2億トン×0.65=1.3億トン
B国の場合:8億トン×0.3=2.4億トン
計算の結果、B国がA国より1.1億トンも輸出量が多いことがわかりました。このようにベースとなる量をきっちりと把握してから解きましょう。
6.割合の変換をマスターしよう
この割合の単元は小学校3年生の小数、分数の考えからきています。
- 割合は小数で表すこともありますし、1より大きいこともあります。
- 小数は百分率(%)、歩合(割、分、厘)、分数で表すことができます。
*下のルールを覚えましょう
| 小数 | 1 | 0.1 | 0.01 | 0.001 |
| 百分率 | 100% | 10% | 1% | 0.1% |
| 歩合(ぶあい) | 10割 | 1割 | 1分(ぶ) | 1厘(りん) |
7. 表を利用して百分率と歩合の問題を解いてみよう
それでは問題です。ノートに写してトライしましょう。
①30人の40%は何人ですか?
➁60人の120%は何人ですか?
③36人の25%は何人ですか?
④40人の8割は何人ですか?
⑤50人の3割2分は何人ですか?
⑥40人の12割は何人ですか?
もし解き方が分からない場合は、ご父兄がこの文章問題の「の」は×という意味だと教えてください。また、あたりまえですけれど百分率も歩合も小数に直して計算することも付け加えてください。
では解答です。
①30×0.4=12 12人
➁60×1.2=72 72人
③36×0.25=9 9人
④40×0.8=32 32人
⑤50×0.32=16 16人
⑥40×1.2=48 48人
8.□を使った問題にトライ
つぎの問題もノートに写してトライしましょう。まず初めに□を使って式をたててください。
①□kgは300kgの5割6分です。
➁260人の6割は□人です。
③□円は4000円の120%です
④84個は□個の140%です。
⑤□ページの8割は96ページです。
⑥750円は□円の25%は何人です。
では解答です。
①□=300×0.56 300×0.56=168 168(kg)
➁260×0.6=□ 260×0.6=156 156(人)
③□=4000×1.2 4000×1.2=4800 4800(円)
④84=□×1.4 84÷1.4=60 60(個)
⑤□×0.8=96 96÷0.8=120 120(ページ)
⑥750=□×0.25 750÷0.25=3000 3000(人)
9.練習問題
①A組の男子の人数はB組の男子の人数の3/5です。B組の男子を45人とするとA組の男子の人数は何人ですか。
②靴下を700円で販売したところ原価の2/5の利益があった。原価はいくらですか。
③3000円のフリースをX割引で購入し1800円を支払った。Xを求めましょう。
④X円の7割引きは300円です。Xを求めましょう。
⑤X人の30%は390人です。Xを求めましょう。
解答
①B組の男子の人数のB組の男子の人数がポイントです。
のは×なのでB組の男子の人数45人に3/5をかけると(45×3/5=27) 答え 27人
②原価を1と考えると売価は原価×(1+2/5)となります。
X×(1+2/5)=700 X×7/5=700 X=700÷7/5 X=700×5/7 X=500 答え 500円
③X割引とは売価を1と考えたときにその1からX割を引いたものです。
この場合は割引された1800円を売価である3000円で割ると、売価の何割で売ったものかがわかります。
1800÷3000=0.6 つまり売価の6割で売った商品なので1=10割から6割を引いて4割引きで売ったことがわかりました。答え 4
④X円の7割引きはX×(1ー0.7)で表せます。
よって式はX×(1ー0.7)=300 X×0.3=300 X=300÷0.3 X=1000 答え 1000
⑤読んだ通りに式を作ります。X×0.3=390 X=390÷0.3 X=1300 答え 1300
10.まとめ
割合をマスターするためにはイメージ、公式、割合の変換、そして問題演習といった流れで学習されることがベターであることを確信しいてます。