展開図をマスターしていきましょう。組み立てたとき、どの点とどの点が合わさるのか。また立体を切断したとき展開図ではどこが切り取られたのか検討していきます。今回もご父兄の指導法のポイントをいくつかご紹介します。
読んでほしい対象児童は4、5年生です。また展開図をどう教えたらよいのかコツを知りたいご父兄方々もそうです。
1.展開図から重なる頂点を読み取る

展開図から立方体を作るとき頂点の重なるところを考えてみましょう。
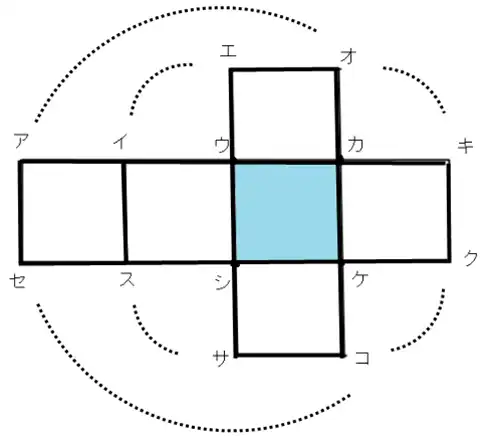
お母さんとサラちゃんの会話例

箱のもとになる厚紙を用意してください。1辺を5cmにして作りましょう。
* 縦と横がそれぞれ何cm必要か考えさせてから、定規を使って平行線や垂直な線を引くようにさせてください。

縦は15cm、横は20cm必要です。

作れましたね。それでは作った厚紙の上にアからセまで 書き入れましょう。次は文字が見えるようにして折り曲げてください。

箱ができました。

箱の角を頂点と言います。また頂点から頂点までを辺と言います。覚えてね。では折ったところを少し開いてみてどの記号と記号が合わさったか見てください。
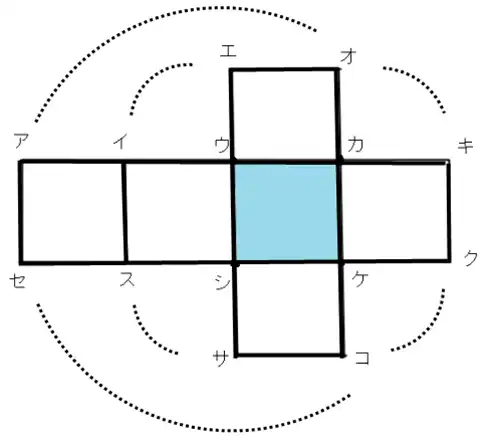

はい。イとエ、オとキ、クとコ、サとス、全部で4つです。

上のふたの部分も見てね。

えーと。アとオとキ、セとコとクです。全部で6つです。

たいへんよくできました。サラちゃん、厚紙を折って確かめなくても分かる方法があるのです。まず、作ってくれた図を展開図といいます。この図のブルーの部分の4つの角を1つ1つ検討します。
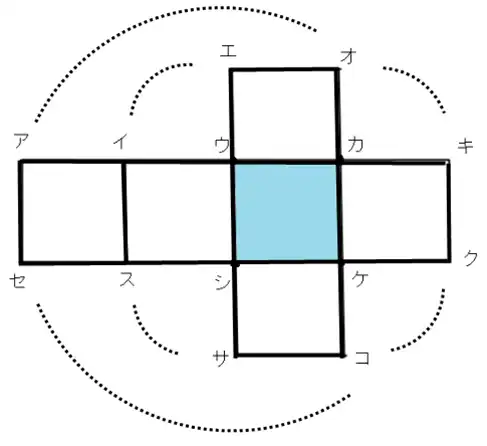

ウからでいいですか。

はい、それではウからイまでの距離を1と考えると、他に距離が1であるところはどこですか。

ウからエです。

すると、イとエが同じ距離にあるので合わさると考えます。残り3つも同じ考え方です。
では、アとオはどう考えたらいいのでしょう?

ウからの距離がどちらも2だからです。セとコも同じ考えです。

まとめると、点ウ、点カ、点ケ、点シから距離が1と2のところを考えればいいことが分かりました。

お母さんはいつでもグレイト!
2.展開図から切断面を読み取る

これから展開図と切断面について考えていきましょう。
初めは立方体から三角錐を切り取る場合です。
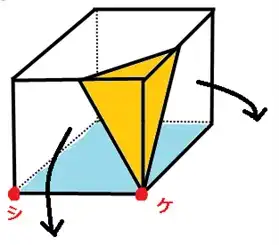

次に立体図を展開図にしてみました。そして切り取った部分がどこなのか切れ込みを入れてみましょう。
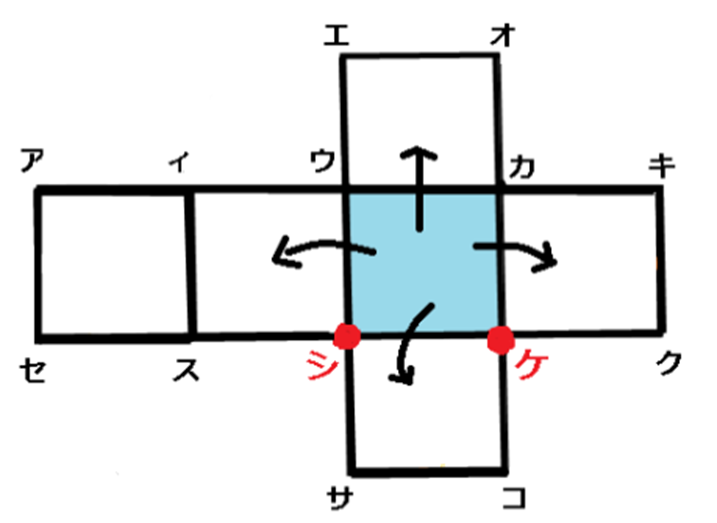

これから展開図の中に線を引くポイントを教えます。
点ウ、カ,ケ、シのような角を基準にして等距離の位置を見つけます。
立体図を見ると、ケから上に進み左右に分かれた2点を a,bとします。
展開図のケを基準にして右を通り1.5進むとa点に到着、そこからケに線を引きます。1本できあがりです。
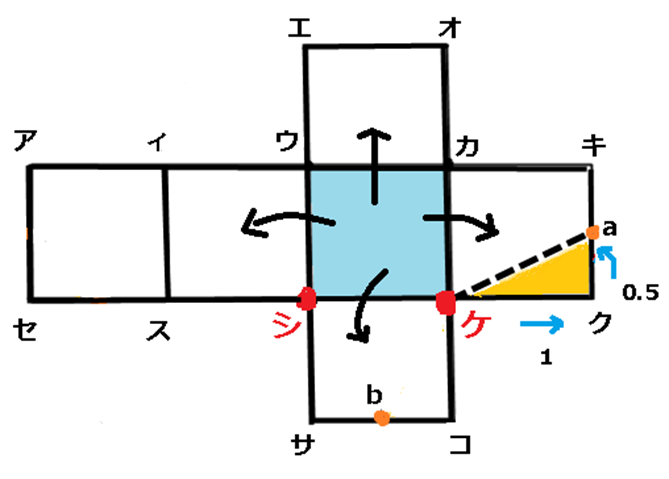

わたしもできます。ケを基準にして下を通り同じく1.5進んだところが点bです。そこからケに線を引きます。2本目が引けました。同じ距離を進む考えですね。
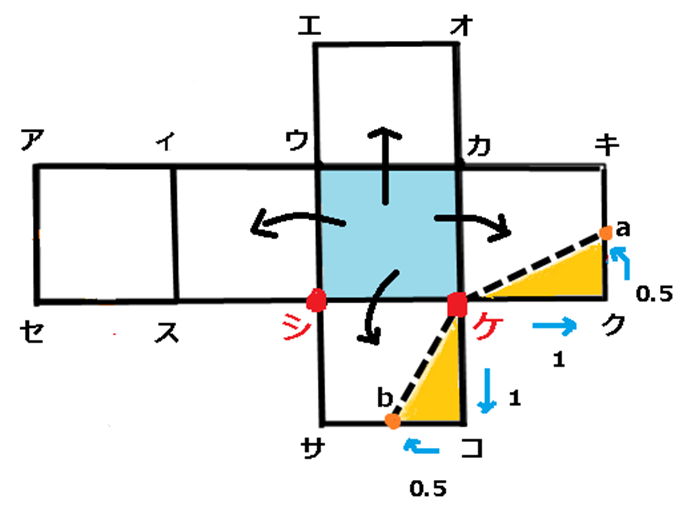

そうです。今度は上のふたの線をつけましょう。シを基準にしてやってみてください。

シから下に進み1.5のところがbになるのでbと重なる点はシから左に1.5進んだところです。ここもb点とします。そうすると、立体図の上の三角形は二等辺三角形なので自動的に点aが決まります。そして、点bから点aに線を引きます。これで3本目が引けました。
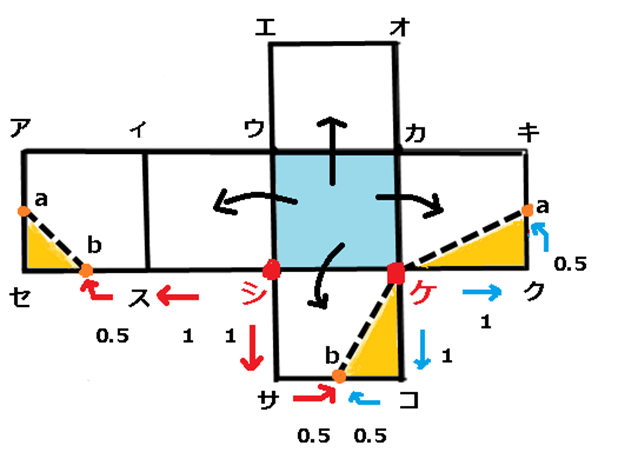

よくできました。マスターしましたね。切り取られた面は二等辺三角形になります。
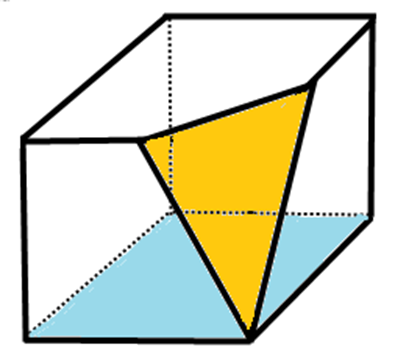

続いて立方体から正三角錐を切り取る場合です。


まず、展開図を作ってみましょう。つぎに、切り取った部分がどこなのか切れ込みを入れてみましょう。
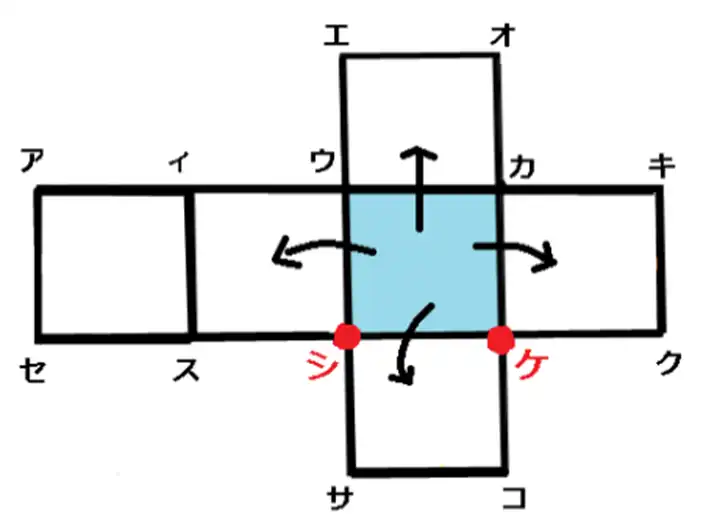

線の引き方のポイントは前回と同じです。点ウ、カ,ケ、シのような角を基準にして等距離の位置を 見つけることでした。
立体図を見るとケから上に進み左右に分かれいます。距離はどちらも2です。点キと点サからケに向かって線を引きます。一度に2本引けました。
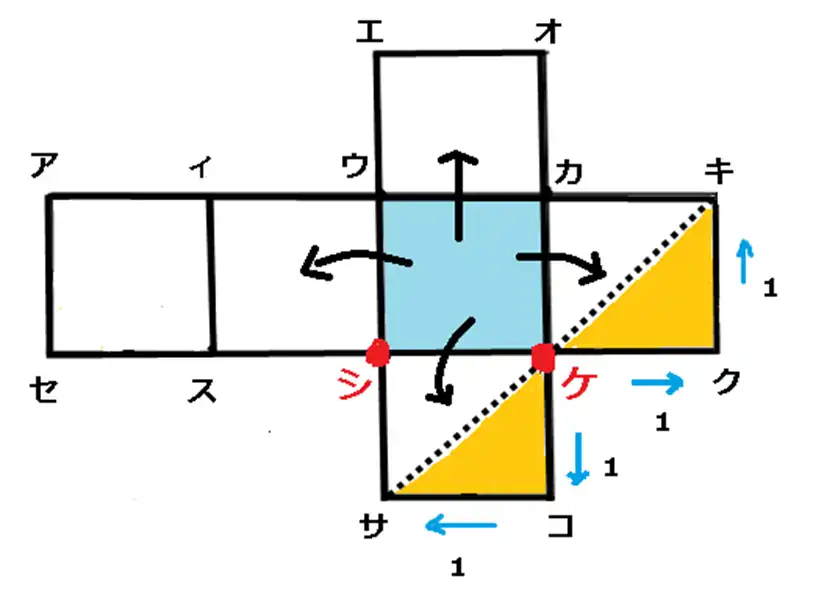

残りは私にやらせてください。シを基準にして距離1は点サです。ここに重なるのが距離1のスです。後は対角線を点スから点アに向かって引くだけです。これが3本目です。
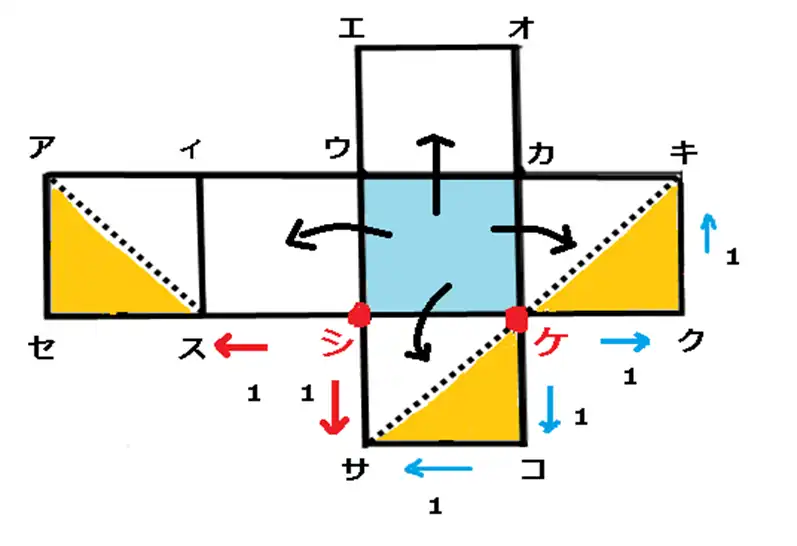

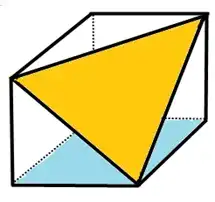
今度は距離が2でしたね。切り取られた面はどんな形になりますか。

切り取った3つの対角線が正方形の対角線なので等しい長さになるので正三角形になります。

そうですね。理由もきちんと発表できているのですばらしいです。
3.まとめ
空間認識力の優れた方は頭のなかで考えられるそうですが、一般的にはねんどを用意されて上の図のように削ってみたり、直したりしたほうが良いと思います。
それと同時に展開図と見比べて何度も何度も確認してみてください。それを繰り返すことで、ついには頭にうかぶようになります。しばらくの間はねんどと展開図との格闘ですね。