1. A点から引いた2つの接線は長さが等しい

これから点Aから円に接線を2本引くと接点までの長さが等しいことを検討していきます。どうしてAから接点までの2本の直線が等しいと分かるのでしょうか?このような疑問を持ったことはありませんか。このことを以下で証明したいと思いますのでご覧ください。
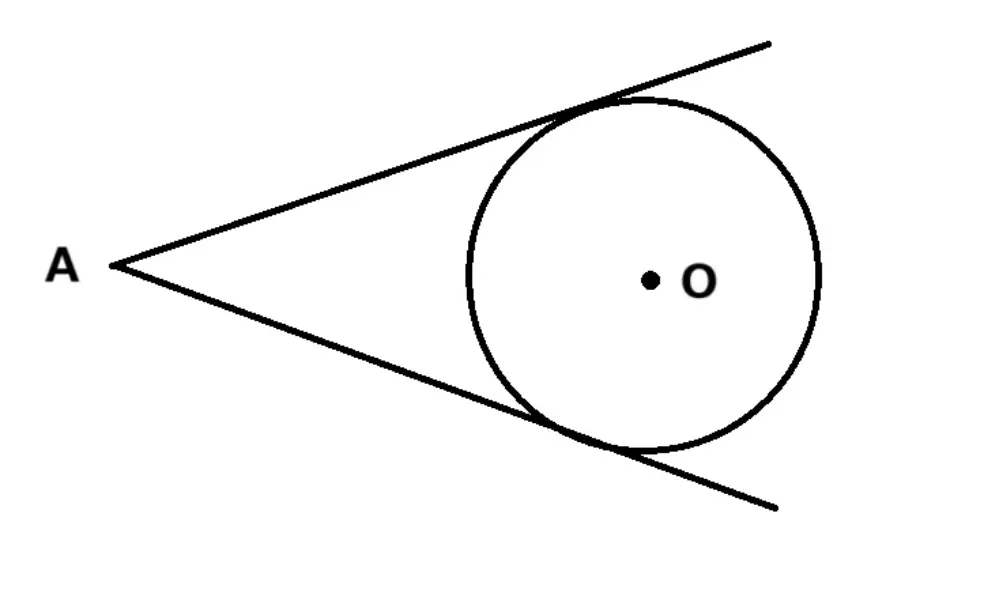

以下がヒントです。
- まずB、Cと記号を付けます。
- つぎに△ACOと△ABOの2つの三角形の合同について考えます。
- 最後に合同が証明できればそれぞれの辺の長さが等しいので証明は終わりとなります。


△ACOと△ABOの合同の証明をします。
- ∠ACO=∠ABO(接線と接点から中心Oに引いた直線のなす角は90°)…①
- CO=BO(半径)…②
- AO=AO(共通の辺)…③
①➁③により斜辺と他の1辺がそれぞれ等しいので△ACO≡△ABO
△ACO≡△ABOによりそれぞれの辺が等しいのでAC=ABとなります。
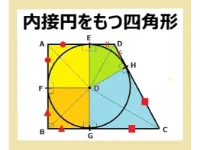
2.上の辺+下の辺=左サイドの辺+右サイドの辺

内接円がある四角形をみるときは4点(点A、B、C、D)からの接線は接点までの長さが等しい。まずこれを検討します。
- Aから引いた2つの接点までの長さが等しい。
- Bから引いた2つの接点までの長さが等しい。
- Cから引いた2つの接点までの長さが等しい。
- Dから引いた2つの接点までの長さが等しい。


上記の4点の中から辺AE=辺AFの証明をしたいと思います。
△AEOと△AFOの合同の証明によって辺の長さを証明する
- ∠AEO=∠AFO(接線と接点から中心Oに引いた直線のなす角は90°)…①
- EO=FO(半径)…②
- AO=AO(共通の辺)…③
①➁③により斜辺と他の1辺がそれぞれ等しいので△AEO≡△AFO
△AEO≡△AFOによりそれぞれの辺が等しいのでAE=AFとなります。


他の三角形の合同の証明から上記と同様に他の辺の長さの証明ができます。
△AEO≡△AFOと同様に△BFO≡△BGO、△CGO≡△CHO、△DHO≡△DEOとなります。ゆえにBF=BG、CG=CH、DH=DE
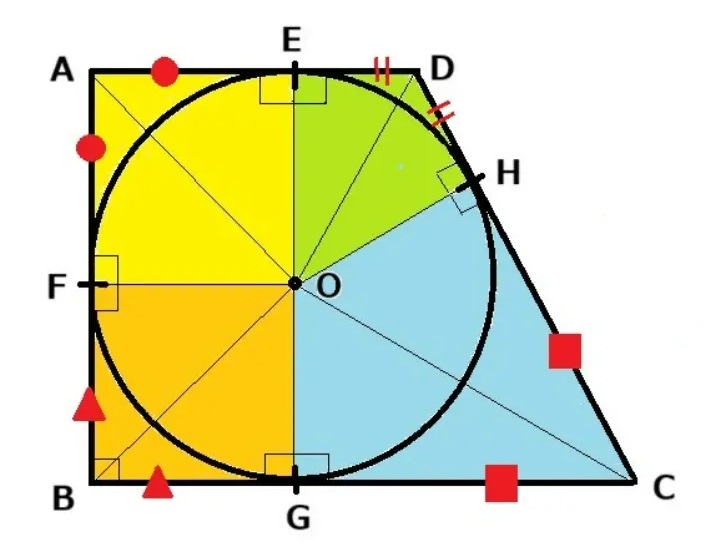

終わりに上の辺+下の辺=左サイドの辺+右サイドの辺の証明をしますので上の図を見ながら確認してください。
上の辺+下の辺=左サイドの辺+右サイドの辺の証明
上の辺:AD=〇+┃┃、下の辺:BC=△+□なので辺AD+辺BC=〇+┃┃+△+□
左サイドの辺:AB=〇+△、右サイドの辺:DC=┃┃+□なので辺AB+辺DC=〇+△+┃┃+□
よって辺AD+辺BC=辺AB+辺DCなので上の辺+下の辺=左サイドの辺+右サイドの辺
3.上の辺+下の辺=左サイドの辺+右サイドの辺を利用した問題

公式を利用して問題1と問題2の辺DCの長さを求めましょう。
問題1

問題2


問題1の解答です。
上の辺+下の辺=左サイドの辺+右サイドの公式より5+8=6+XですのでX=7となります。
答え 7
続いて問題2の解答です。
内接円がある四角形をみるときはある点から接線を引くと接点までの長さが等しい。この定理を利用して解いていきます。
まず点Aから点Bへ目線を移していきますと5cmと5cm、それから点Bから点Cへと移しますと5cmと6cmとなります。続いて点Cから点Dへ進みますと6cmと3cmになります。よって辺DCは9cmです。
答え 9

4.まとめ

注意点を2つにまとめてみました。
- 円に接する2直線の長さは等しい。:2つの三角形の合同を証明する。
- 内接する円がある四角形は上の辺+下の辺=左サイドの辺+右サイドとなる。:4組の三角形の合同を証明する。
これらの証明を書けるようにしましょう。