1.二次関数と面積

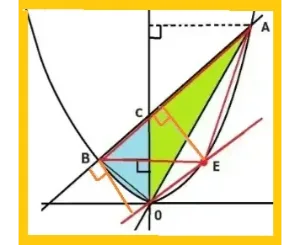
ケン君、これから二次関数と直線で囲まれた△ABOの面積をもとめたいと思います。
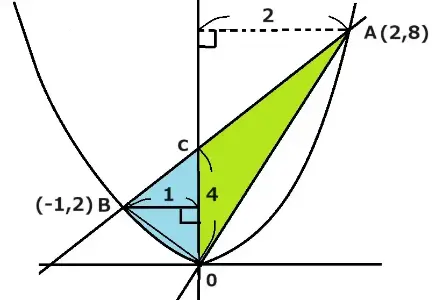
二次関数の式はy=2X2で直線ABはy=2X+4です。まず初めにA、Bの座標を求めましょう。

はい、わかりました。y=2X2とy=2X+4を連立方程式の代入法でやってみます。
すると2X2=2X+4となり、左に移行します。2X2ー2Xー4=0 この式を2で割ります。X2ーXー2=0となったので因数分解をしてみます。
(Xー2) (X+1)=0となったので X=2,-1です。X=2を上の式に代入するとy=8となり、Aの座標は(2,8)です。
もう1つのX=-1を上の式に代入するとy=2となり、Bの座標は(-1,2)と決まりました。
これで面積を求めるための準備ができましたので数字をグラフに記入します。
底辺を4、高さは左と右の三角形(1+2)を合わせて3なので式は4×3÷2=6 答えは6です。

高さをまとめた考えはグッドです。ではつぎに進みましょう。

はい、つぎは何かな。
2.二次関数と円錐の体積

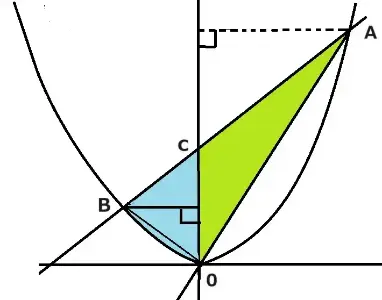
△ACOをy軸を軸として1回転させたときの体積を求めましょう。二次関数の式はy=2X2で直線ABはy=2X+4です。
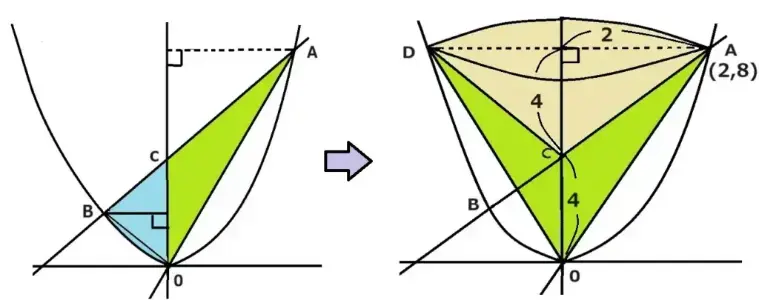

右図のように空洞ができた逆さまな円錐になると思います。ですから全体の円錐から空洞の部分を引きます。
円錐の体積の公式は半径×半径×π(パイ3.14)高さ×1/3なので、まず大きい円錐の体積は2×2×Π×8×1/3=32π/3です。
つぎに空洞の円錐の体積は2×2×Π×4×1/3=16π/3です。最後に引き算をします。32π/3-16π/3=16π/3 答 16π/3㎤

よくできました。では、つぎの問題です。
3.三角形を2等分する直線の求め方

今度は点Aを通る直線で△ABOを2等分します。そのときの直線の式①を求めましょう。二次関数の式はy=2X2で直線ABはy=2X+4です。
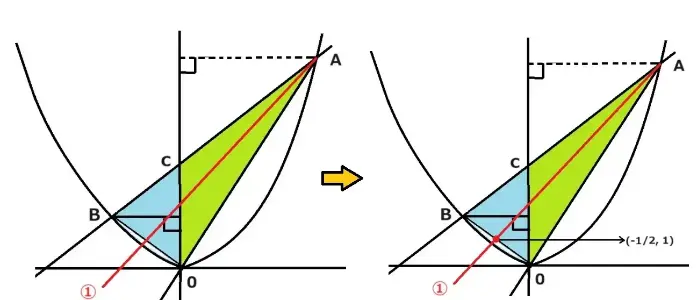

2等分線をもとめるのには直線BOの中点を求めます。点Bの座標は(-1,2)で原点( 0,0 )なので中点を求める公式を使います。
点BのⅩ座標と原点のⅩ座標をたして2で割ります。同様に点BのY座標と原点のY座標をたして2で割ります。すると中点の座標は (-1/2,1)になりました。

それからどうしますか。

はい、中点の座標(-1/2,1)と点Aの座標(2,8)をy=aX+bの式に代入して連立方程式で解きます。
代入しますと1=-1/2a+b, 8=2a+bとなり、これを解きます。a=14/5 , b=12/5です。これをy=aX+bにいれて完成です。 答え y=14/5X+12/5

つぎは点Bを通る直線で△ABOを2等分します。そのときの直線②の式を求めましょう。二次関数の式はy=2X2で直線ABはy=2X+4です。
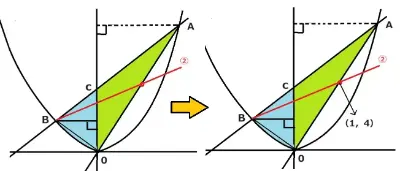

先ほどと同様に2等分線をもとめるのには直線AOの中点を求めます。
それは直線AOを三角形の底辺とみたてて底辺の長さを同じにすれば高さは同じなので面積が等しくなるからです。
点Aの座標は(2,8)で原点(0,0)なので中点を求める公式を使います。
点BのⅩ座標と原点のⅩ座標をたして2で割ります。同様に点BのY座標と原点のY座標をたして2で割ります。すると中点の座標は (1,4)になりました。

つぎはどうしたら良いですか。

はい、y=aX+bの式に中点の座標(1,4)を代入します。また点Bの座標(-1,2)をy=aX+bの式に代入すると4=a+b , 2=-a+bとなりました。
これらを連立方程式で解くとa=1 , b=3となりました。a , b をy=aX+bにいれて完成です。 答 y=X+3

3番目は原点を通る直線で△ABOを2等分します。そのときの直線③の式を求めましょう。二次関数の式はy=2X2で直線ABはy=2X+4です。
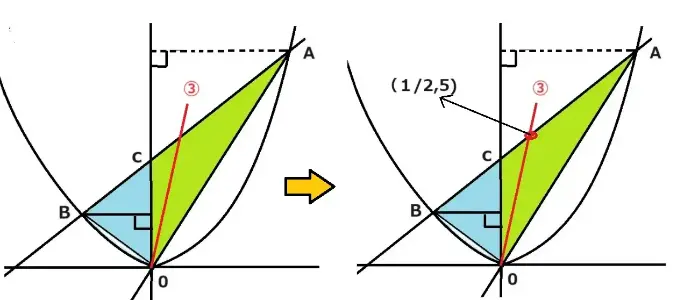

こんどはどうですか。

つぎも同じです。底辺をABとみたてて中点を求めると(1/2,5)となりました。2等分線は原点を通りますから③の直線の式はy=aXに(1/2,5)を代入するとy=10Xとなりました。答 y=10X
4.少し難易度が高い2等分線の求め方

最後にCを通って△ABOの面積を2等分する直線の式を求めましょう。二次関数の式はy=2X2で直線ABはy=2X+4です。これは中点を求める方法では解けません。それでは、どういう考え方が必要になるでしょう。
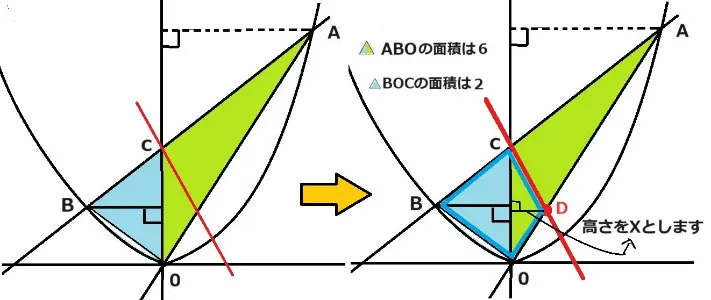

はい、△ABOの面積は6でした。直線CDで2つの図形に分けられます。その1つが四角形CBODです。
この四角形はさらにy軸で2つの三角形に分けられます。これらの2つの三角形の面積が△ABOの面積の半分の3であれば良いわけなので式を作ってみます。
4×1÷2+4×X÷2=3 4×1÷2は△BOCを求める計算式で4×X÷2は△DOCの面積の式です。この2つの計算式を合せたものが上の(4×1÷2+4×X÷2=3)式です。
計算すると2+2X=3 2X=1 X=1/2 この答えを直線AOの式y=4Xに代入するとy=2となりました。
これで点Dの座標は(1/2,2)です。点Cの座標は(0,4)です。これらをy=aX+bに代入すると点Cよりy=aX+4と表すことができます。
これに点Dの座標を代入するとa=-4となりました。よって求める式はy=-4X+4です。 答え y=-4X+4
全体的には考え方が同じですがもう少し簡単にできます。△BOCの面積は2ですので△DOCの面積1となります。これで4×X÷2=1として計算しても良いと思います。

そうですね。少しでもアイディアがあれば言ってください。この問題は共有する底辺がありませんので面積を半分にしてから残りの三角形の面積を考える方法を見つけたのはとっても良かったと思います。その調子で頑張りましょう。

はい、わかりました。

つぎは等積変形を利用した直線の式を求める問題です。
5.等積変形を使った直線の式の求め方

△ABEが△ABOと等しい面積になるようにy=2X2上に点Eをとり、その際の点Eの座標と直線EOの式を求めなさい。直線ABはy=2X+4です。
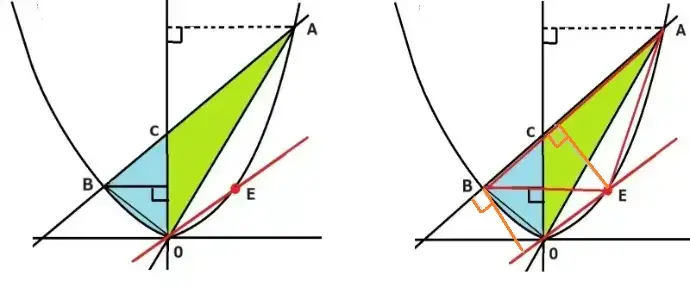

この問題は底辺を辺AB、高さも等しい三角形と考えます。高さを同じにするためには直線ABと直線EOが平行な直線でなければなりません。
つまり、直線ABの傾きは2とでているので直線EOも2とわかります。答え y=2X 点Eの座標はいま求めたy=2Xとy=2X2を連立方程式の代入法で解きます。
すると2X2=2Xとなり移行させますと2X2-2X=0となります。因数分解しますと2X(X-1)=0となります。
これを解きますとX=0, 1です。X=1をどちらかの式に代入しますとy=2となりました。答え(1,2)

よくできました。
等積変形は2つの要素をおさえておけば大丈夫です。1つは共通な辺はどれか。この場合は辺ABでしたね。もう1つは高さを等しくするために辺ABと傾きが同じになれば良いことでした。
たいてい直線ABは座標が与えられていて直線の式を求めなければなりませんが、この問題に限り最初から直線の式がわかっていたのでらくでしたね。

そうですね。考え方の勉強だと思いました。
6.まとめ
二次関数の中点を求める公式や等積変形に関する重要な要素2つ(底辺をどこに決めるのか、そして高さを同じにする)を理解したうえで平行な直線を考える問題でした。それをノートに分類しておきましょう。
たとえ高校入試で難しい二次関数の問題が出題されても解決する糸口がつかめるのではないかと思います。