今回は二次関数の座標の設定の順序を示し解法の手順を図や式で示しました。
目線をどこに向けるかでスピー度解決ができるように示しました。
二次関数の基本は設定された座標をｙ＝aX²に代入することです。
そしてまた、縦の長さはY座標の上から下を引くこと、横の長さはX座標の右から左を引くこと、これらの公式をしっかり守りましょう。
そうすることで自然と関数が楽に解けるようになると思います。
クリックできる目次
１．横の長さの比からｙ＝aX２のaを求める
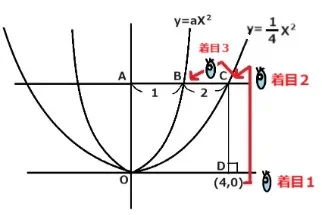
二つの2次関数ｙ＝1/4X2とｙ＝aX２があります。AB:BCが1:2で、ACはX軸に平行です。Dの座標が(4,0)のときaを求めましょう。
着目点：まず初めに、視点をDの座標 (4,0)から出発させて点Cに移してを座標を決めます。
つぎにAB:BC＝1:2を利用してBの座標を求めます。最後にそれをｙ＝aX２の式に代入して求めます。
DはＸ軸上にあるので（4,0）です。つぎにＣのⅩ座標4をｙ＝1/4X2に代入してＹ座標を求めますと４となりました。
こうしてCの座標（4,4）が決まりました。ＡＣ間の長さはDの座標により４とわかりますのでAB:BC＝1:2を利用します。
すると、ABはACの1/3であることがわかるので4×1/3=4/3となりました。これはBのX座標です。Y座標はCのY座標と同じです。
こうしてBの座標（4/3,4）が決まりました。このBの座標をｙ＝aX２に代入するとa=9/4となりました。 答え a=9/4
２．縦の長さの比からｙ＝aX２のaを求める
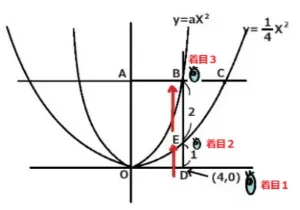
二つの2次関数ｙ＝1/4X2とｙ＝aX２があります。BE:EDが２:1で、ACはX軸に平行です。またBDはY軸に平行です。Dの座標が(4,0)のときaを求めましょう。
着目点：まず初めに、視点をDの座標から出発させてEの座標に移してを座標決め、BE:ED＝2:1を利用してBの座標を求めます。
最後にそれをｙ＝aX２の式に代入して求めます。
点DはＸ軸上にあるので（4,0）です。つぎに点EのⅩ座標4をｙ＝1/4X2に代入してＹ座標を求めますと４となりました。
よって、Eの座標は（4,4）。このことからED間の長さは４とわかりますのでBC:ED＝2:1を利用します。
すると、BDはEDの3倍であることがわかるので４x3=12となりました。これはBのY座標です。
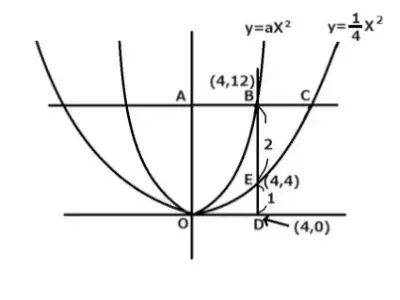
こうしてBの座標（4，12）が決まりました。
この座標をｙ＝aX２に代入すると12＝16aとなり、これを解きますとa=3/4となりました。答え a=3/4
３．縦、横の長さが違う比からｙ＝aX２のaを求める
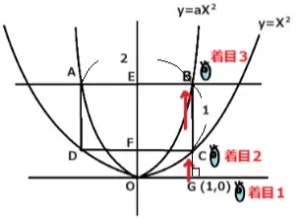
二つの2次関数ｙ＝X2とｙ＝aX２があります。AB:BCが２:1で、ABはX軸に平行です。またBGはY軸に平行です。Gの座標が(１,0)のときaを求めましょう。
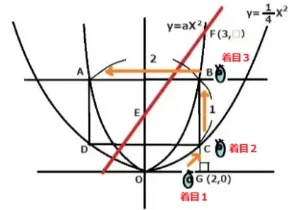
着目点：まず初めに、視点をGの座標から出発させてCの座標に移してを座標決め、そのあとBの座標をaを使って決めます。
Bの座標が決まったら、BのY座標からCのY座標を引き算します。
そして、BC間の長さがAB:BC＝2:1なので、それを利用してBの座標を求めます。
最後にそれをｙ＝aX２の式に代入して求めます。
GはＸ軸上にあるので（1,0）です。つぎにCのⅩ座標１をｙ＝X2に代入してＹ座標を求めますと１となりました。
よって、Cの座標は（1,1）。つぎにBのX座標１をｙ＝aX２に代入しますとY座標はaと決まりました。したがいまして、Bの座標は（1,a）。
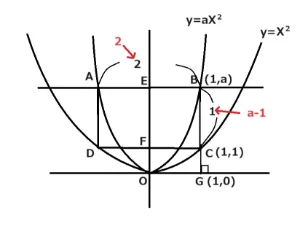
このB,CのY座標を使ってBCの長さを求めます。BのY座標からY座標を引きますとa-1とわかりました。
最後にAB:BC＝2:1なのでEB:BC=1:1です。よって、a-1＝１ a=2となりました。答え a=2
４．正方形の点Bを通る二等分線を求める
二つの2次関数ｙ＝1/4X2とｙ＝aX２があります。四角形ADCBは正方形です。辺ABはX軸に平行で、辺BCはY軸に平行です。
Eの座標が(２,0)のとき正方形を２等分する直線の式を求めましょう。
着目点：まず初めに、視点をEの座標から出発させて点Cに移してを座標決め、AB:BC＝1:1を利用してBの座標を求めます。
つぎにDの座標を決めます。最後にB,Cを通る直線の式を求めます。
E座標はＸ軸上にあるので(2,0)です。つぎに点EのⅩ座標2をｙ＝1/4X2に代入してCのＹ座標を求めますと1となりました。
よって、Cの座標は(2,1)となりました。またCDの長さは４とわかります。
一方、Bの座標はX座標が２ですのでｙ＝aX２に２を代入します。すると、Y座標は４aとでました。
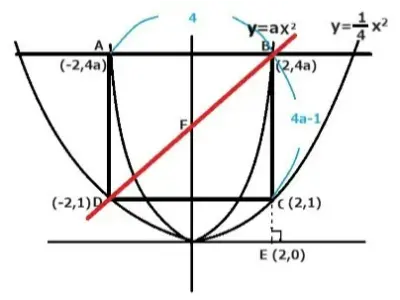
こうして点Bの座標（２,4a）が決まりました。BのY座標からCのY座標を引き算しますと４aー1となり、BCの長さが決定です。
正方形ですから４a－１＝４、これを解きますとa=5/4 です。
つぎに、y=5/4X2にBのX座標２を代入するとY座標が５とでました。これでB座標は(2,5)となり、残りはD座標を求めるだけです。
D座標はC座標と反対側なので(-2,1)なります。正方形は対角線で面積を2等分できますのでｙ=aX+bの式にB座標とD座標を代入して連立方程式で解きますとy=X+3となりました。 答え y=X+3
５．F座標を通って長方形の面積を二等分する直線を求める
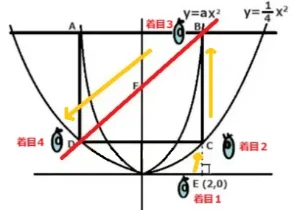
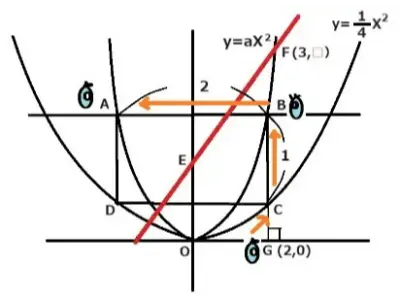
二つの2次関数ｙ＝1/4X2とｙ＝aX２があります。四角形ADCBは長方形です。辺ABはX軸に平行で、辺BCはY軸に平行です。AB:BC＝2:1です。
Gの座標が(２,0)でFの座標が(3,□)のときFを通って長方形を２等分する直線の式を求めましょう。
着目点：まず初めに、視点をGの座標から出発させて点Cに移してを座標決め、AB:BC＝2:1を利用してBの座標を求めます。
つぎにそれをｙ＝aX２の式に代入してaを求めます。すると、FのY座標が求まります。
最後は点Fと点Eの座標をｙ＝aX＋ｂに代入して連立方程式で解きます。
G座標は(2,0)なのでCのX座標は２です。これをｙ＝1/4X2に代入するとY＝１となりました。C座標は(2,1)です。
これでB座標のX座標は２なのでｙ＝aX２に代入してｙ＝４aを求めます。
そしてB座標(2,4a)が決まりましたので辺BCを4aー1で表します。
辺CDは４ですのでその半分が辺BC4aー1と等しくなります。
これを式にしますと4aー１=2、解きますとa＝3/4です。
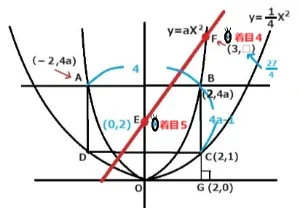
すると、y=aX2はy=3/4X2となりましたのでFのX座標３を代入してY座標を求めます。
F座標は(3,27/4)です。面積の二等分線を決めるときは四角形の対角線が交わったところに線を引きます。この場合はE座標です。よってE座標は(0,2)とわかりました。
最後にE座標、F座標をｙ＝aX+bの式に代入して連立方程式で解きます。a=19/12, b=2 よってy=19/12X+2です。 答え y=19/12X+2
６．まとめ
いかがでしたでしょうか。座標の設定の順序を示しながら解法の手順を図や式で説明してみました。
二次関数の基本は示された座標をもとにｙ＝aX²に代入することです。
そしてまた、縦の長さはY座標の上から下を引くこと、横の長さはX座標の右から左を引くこと、これらの公式をしっかり覚え、活用しましょう。
これらの問題から二次関数の面積や体積の問題へと発展しても基本がしっかりしていれば大丈夫です。
