内接円とは三角形やその他の多角形に内接している円のことです。高校入試の観点からは角度や半径についてよく出題されます。
1.内接円の描き方

これから内接円の描き方を解説します。まず初めに角の二等分線の書き方から説明します。簡単なので是非覚えましょう。
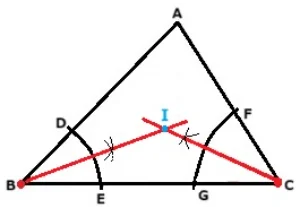
二等分線の描き方
- まず点Bにコンパスの針を刺し、点D、点Eとなる線を描きます。
- 次に点Dに針を刺し線を描きます。点Eも同様にします。
- そして線が交わったところに点Bから直線を引きます。
- 続いて点Cも同様の作業をします。
- これで角の二等分線の出来上がりです。

内接円の描き方
- 三角形ABCを描きます
- 頂点Aの角の2等分線を引きます
- 頂点Bの角の2等分線を引きます
- 図では3本の2等分線が引いてありますが2本の交点で内心Iが決まります
- コンパスの針をIに刺して3辺に接するように円を描きます
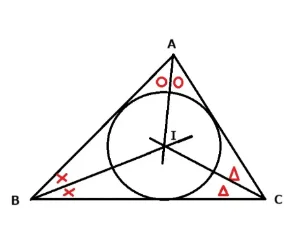
2.どうして内心の角度から90°を引いて2倍すると頂角が求まるのか

これから内心の角度から90°を引いて2倍すると頂角が求まる理由を解説します。
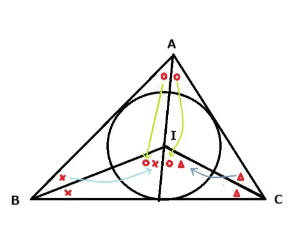
理由
三角形ABCの内角(180°)は〇〇✖✖△△でできています。その半分である〇✖△は90°です。内心の角度∠BIC=〇〇✖△なので90°+〇で表せます。
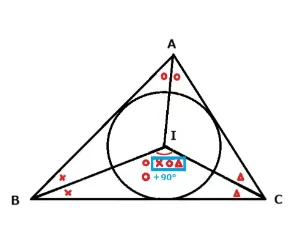
∠BIC=90°+〇から90°を引くと〇が残ります。頂角Aは〇〇なので(∠BIC-90°) ×2になります。すると次のような公式が生まれます。
頂角A=(内心の角度∠BIC-90)×2

これから内心の角度から90°を引いて2倍すると頂角が求まる理由を解説します。
まず初めに上の式の左辺と右辺を入れ替えます。
(内心の角度∠BIC-90)×2=頂角A ⇒ 2で割ります(内心の角度∠BIC-90)=頂角A/2
⇒ 90を移行します 内心の角度∠BIC=頂角A/2+90
このようにして式が変形されて公式ができました。
内心の角度∠BIC= 頂角A/2+90

公式を利用してつぎの練習問題に取り組んでください。
練習問題1
内心の角∠BIC=120°のとき頂角Aの角度X°を求めなさい。


これから公式を使った場合と公式を忘れた場合の2つの解説をします。
解説
*頂角A=(内心の角度∠BIC-90)×2を使う場合
頂角A=(120-90)×2=60 答え 60°
*公式を忘れた場合の解法
まず△IBCに着目します。内心の角度∠BIC=120°なので残りの角×△は60°です。
つぎは∠ABCと∠ACBに目を移します。すると××△△で成り立っていることがわかります。×△は60°なので××△△はその2倍の120°です。
最後に頂角Aは180°から120°を引くと60°と出てきます。 答え 60°
練習問題2
頂角Aが50°のとき内心の角∠BICを求めなさい。


練習問題1と同様に2つの解法を示しました
解説
*内心の角度∠BIC=頂角A/2+90の公式を使う場合
内心の角度∠BIC=50/2+90=25+90=115 答え 115°
*公式を忘れた場合の解法
まず△ABCに着目します。頂角A=50°なので残りの角∠ABCと∠ACB(××△△)は130°です。
つぎは△IBCに目を移します。∠IBCと∠ICBは×△で成り立っていることがわかります。×△は130°の半分なので65°です。よって180°から65°を引けば∠BICが求められます。よって115°となります。 答え 115°
3.内接円の半径の求め方

3辺の長さと面積がわかっているとなぜ内接円の半径を求めることができるのか解説していきます。それを下図で検討していきましょう。
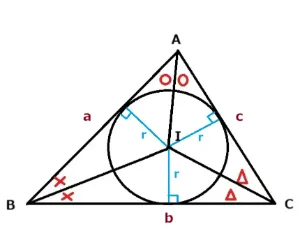
解説
まず初めに△ABIの面積から求めましょう。底辺はaで高さはrなのでar/2で表せます。同様に△BCIもbr/2となり、さらに△CAIもcr/2で表せました。
これら3つの面積を合せると△ABCの面積=ar/2+br/2+cr/2となります。この式を半径を求める式に変形していきます。
まず左右を入れ替えます。ar/2+br/2+cr/2=△ABCの面積
つぎに左右に2を掛けます。するとar+br+cr=2×△ABCの面積に変化します。そして左辺の共通であるrを()の外に出しました。r(a+b+c)=2×△ABCの面積
もう一つの作業で終了です。両辺を(a+b+c)で割ります。最終的には次のようになりました。
r=2×△ABCの面積/a+b+c
このようにして式が変形され公式ができました。これで半径が求まります。いかがでしたか。
練習問題

ではつぎの問題に挑戦です。
各辺が6cm、8cm、10cmの直角三角形があります。このとき内接円の半径を求めなさい。
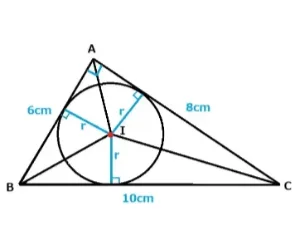
解説
*r=2×△ABCの面積/a+b+cの公式を使う方法
△ABCの面積は6×8÷2=24、各辺の長さを合せると6+8+10=24になるので公式にこれらの数字を入れます。
r=2×24/24=2 答え 2cm
*半径rを使って3つ辺の長さから求める方法
数学カテゴリーの【高校入試】内接円の半径を求める2パターン&二次関数の面積、体積、二等分線、等積変形を解説にあります。是非ご覧ください。
4.まとめ
今回の公式をまとめてみました。是非覚えてください。とても便利ですよ。
- 三角形の頂角を求める公式:頂角 =(内心の角度∠BIC-90)×2
- 三角形の内心の角度を求める公式:内心の角度∠BIC = 頂角A/2+90
- 三角形の内接円の半径を求める公式:r = 2×△ABCの面積/a+b+c