【５年生基礎】対角線から三角形の数で内角の和を求める公式や対角線を求める公式まで踏み込みました

正５角形の書き方を円と分度器を使って書いてみましょう。

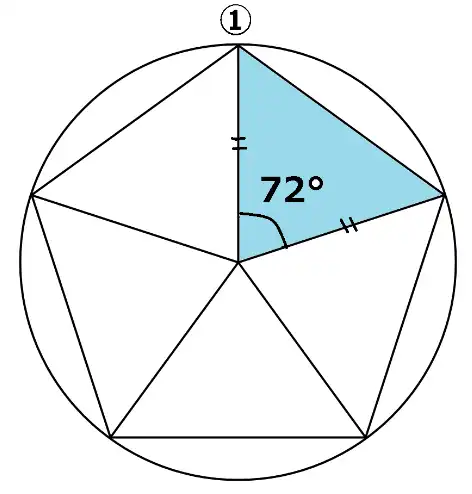
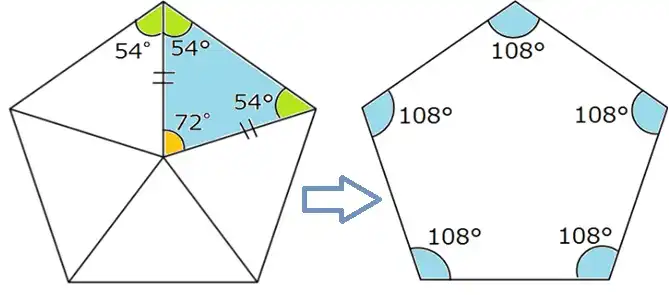
図のように正5角形は二等辺三角形が5つで構成されています。ブルーの部分の三角形を見てください。

半径と半径ではさまれた角度は72°です。円は360°ですから5でわったものが72°です。よって頂角が72°の二等辺三角形であることがわかりますね。

分かります。

次は分度器のセットの仕方です。

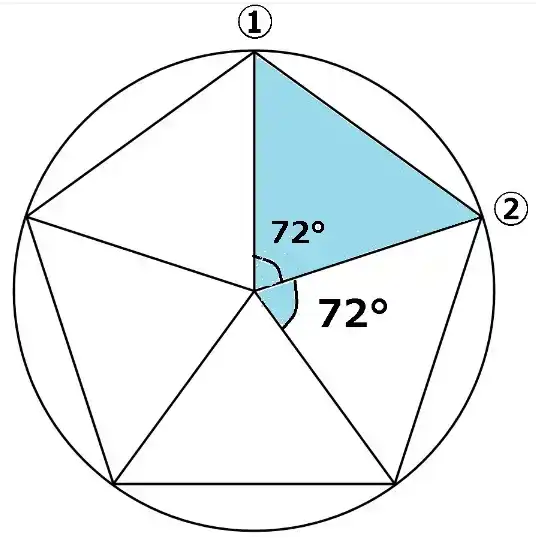
初めに①と中心に向かう線を引きます。それに沿って分度器を置き、円の中心に分度器の中心がくるようにセットします72°を測ったら➁と印を付けてください。

つぎは②と中心に沿って分度器をセットして①と同様に72°を測ったら円周に③と印をつけます。

このようにして③、④、⑤と印をつけます。最後に印を線で結べば正五角形ができます。

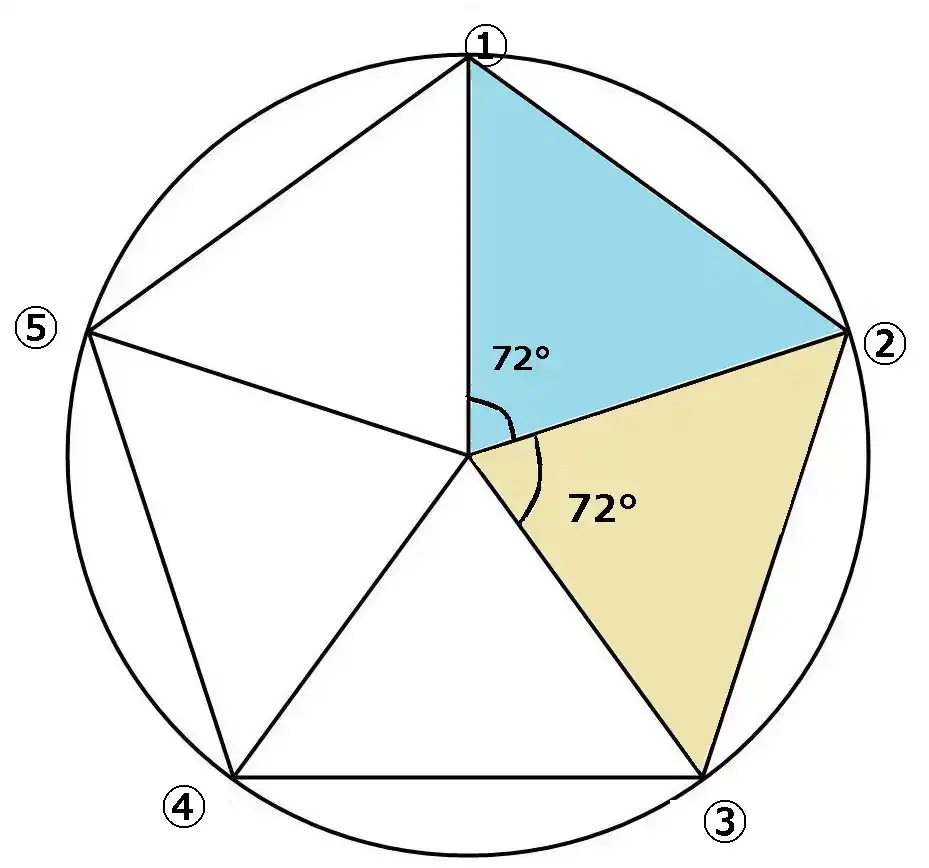
角度はご覧の通り底角が54°の二等辺三角形５こが集まって正５角形になっていることがわかりますね。それでは中心に向かう線を消してみましょう。１つの内角は三角形の底角54°が２つ集まったものですね。

すると、1つの内角は108°になりました。それが５つあるわけですから108×5＝540となります。したがって、５角形の内角の和は540°となります。

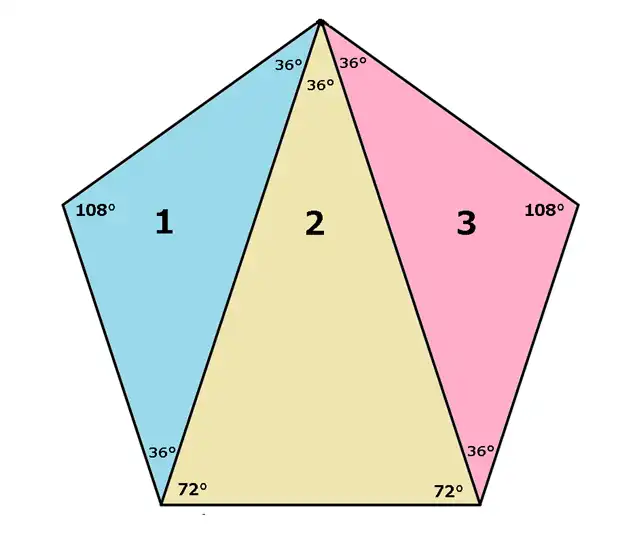
頂点から対角線を引いて内角の和について考えてみましょう。５角形は１つの頂点から２本対角線が引けます。すると三角形が３つできましたね。よって、三角形の内角の和は180°なので180×３＝540　５角形の内角の和は540°になりました。

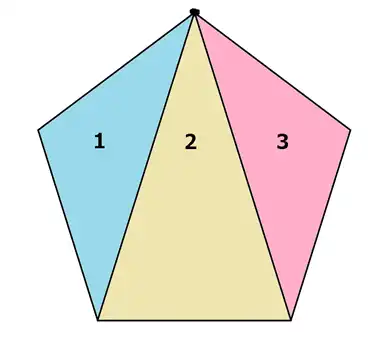
その他分かったことがあります。１と３の三角形は合同（ぴったりと重なる）な二等辺三角形であることがわかります。２は１と３とは形が変わりますが二等辺三角形です。

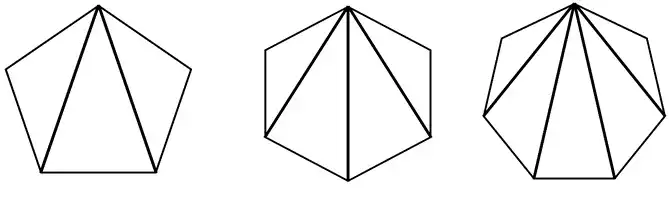
さらに三角形の数から内角の和を考えてみましょう。サラちゃん、どんなことが分かりますか。

はい。５角形は１つの頂点から引いた線によって３つの三角形に分けられ、６角形は４つ、７角形は５つに分けられます。それぞれの多角形の数から２を引いたものが三角形の数になることが分かります。これも表を作ってみて確信しました。

そうですね。N角形の三角のできる数は(Nー2)こです。１この三角形の内角の和は180°ですから（N-2)×180で多角形の内角の和が求められることがわかりました。家族みんなで公式を使って次の問題を解いてみましょう。（解答は５のまとめの後にあります。）

多角形の対角線は何本あるかを考えてみましょう。

５角形は１つの頂点から対角線が２本引けます。

それでは６角形は何本引けますか。また７角形は何本引けますか。（下の図を参考にして考えましょう。）

６角形は３本、７角形は４本対角線が引けます。図と表を作ってみました。

こうすると、いろいろな関係性が分かりやすいです。

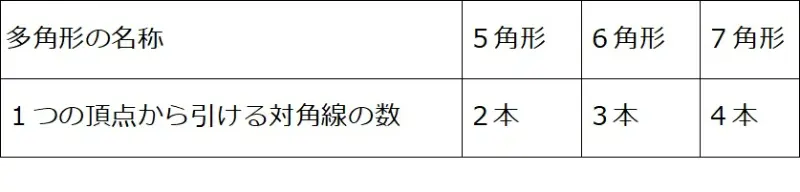
表から分かったことを発表します。５角形、６角形、7角形から３を引いた数が１つの頂点から引ける対角線の数になっています。だから、N角形の頂点の数から３を引いた数が１つの頂点から引ける数だと思われます。よって、N角形の１つの頂点から（Ｎ－3）本の対角線を引くことができる公式が導き出されました。

これらの図や表から導き出した考えは実にすばらしいです。これを利用すると、Ｎ角形の対角線の数はＮこの頂点があるので頂点の数（Nこ）×１つの頂点から引ける対角線の数になるはずです。

自分の図で線を引いたら反対側からも引けました。全部２本ずつになってしまいました。

そうですね。対角線は反対側からも引くので結果的に２回ずつ引くことになります。したがって÷２となります。

まとめるとN角形の対角線の数＝N×(N-3)÷２で求められます。これはとても大切な公式です。是非覚えておいてください。家族みんなで公式を使って次の問題を解いてみましょう。（解答は５のまとめの後にあります。）