公倍数、公約数をマスターすると数字に対する意識が芽生えて感覚が鋭くなります。例えば51をみたら3と17で割れるとか87をみたら3と29で割れるとすぐに分かるようになります。
一般的には51や87といった数字は素因数分解などの練習をしていない限り何で割れるかすぐには思い浮かびません。
このように普段から公倍数、公約数など数字にふれていれば少しずつの練習で効果がみられると思います。
教え方に興味(平均や単位量あたりの大きさ)があるご父兄の方々是非お読みください。また、今までの学習の復習としても幅広い学年の方に役に立つと思います。
1.倍数と公倍数
*倍数とは
ある数に何倍も掛けたものです。
*倍数の指導法
お子様に掛け算九九の7の段いえると尋ねれば当たり前のようにYESと答えます。
しかしながら、7の倍数はと問われれば、倍数はどんな数と質問を返してくるお子様がなかにはいると思います。同じ意味ながら言葉が違えば戸惑う場合があります。
まず初めに、7の段と7の倍数は同じだよとしっかり説明してあげること。
つぎに、7×9=63までで終了しないことです。70,77,84,91,98,105,112,119,126,133,140というふうに×20までは覚えましょう。ちなみに×20まで教えている国もあるみたいです。
これらの数字になじむと逆にこれらの数字が7で割れることがすぐに見分けられるようになります。
これはとても便利ですね。ある数字がでてきたらいくつで割れるかが頭の中に浮かぶようになるわけですから、数字に対する感覚がするどくなっているはずです。
*公倍数とは
2つ以上の整数に共通する倍数です。
*公倍数の指導法

2倍、3倍して共通の数を見つける方法をやってみましょう。
例:5と7の公倍数の場合
①5の倍数をいくつかノートに書かせます。5, 10, 15, 20, 25, 30, 35
➁7の倍数をいくつかノートに書かせます。7, 14, 21, 28, 35

共通の数字を見つけたね。これが公倍数です。一番最初に見つけた共通で小さな数を最小公倍数と言います。

次の公倍数は同じように数字を書き続けて見つけるのですか。

公倍数35に2倍、3倍していくとより大きい公倍数が見つかります。

2倍すれば70で、3倍すれば105です。

素因数分解を使って公倍数を見つける方法もあるよ。素数とは2、3、5、7,11のようにその数と1でしか割れない数を言います。
例:36と48の公倍数を小さい方から3つ素因数分解を使って見つけてみましょう。

私にも説明させてください。素数の2、3で割っていきます。すると一番下は3と4になりました。3と4は1以外では割れないのでここで素因数分解は終わりです。
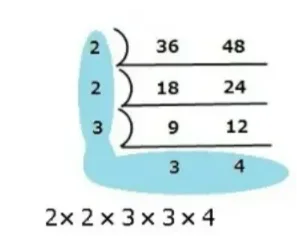

今度はお父さんの番でいいですか。ブルーの部分の数字を全部かけ算します。すると144になります。これが1番小さな公倍数、つまり最小公倍数と言います。この144を2倍、3倍していけば公倍数がどんどん見つかります。
2.約数と公約数
*約数とは
ある整数を割るこのできる整数です。
*約数の指導法
ポイント:公倍数をたくさん練習すると約数が自然とみえてきますし、分数の約分、通分も楽になります。特に2桁の素数の倍数を覚えるとなお良いと思います。
例:13,17,19の見慣れない数字は素数(1とその数でしか割れない数)です。その倍数につていくつかみていきましょう。
13の倍数:13, 26, 39, 52, 65, 78, 91
17の倍数:17,34, 51, 68, 85, 102
19の倍数:19, 38,57, 76, 95, 114

ある数がどんな数で割れるかを見ていくときその割れる数が約数です。具体的に例を見ていきましょう。
例:18の約数の説明

18は1、2、3、6、9、18で割れますね。これら6つの数を約数と言います。
例:72の約数の説明

少し大きな数字になると間の数が抜けやすくなりますが、それを防ぐ方法があるので説明します。
72の場合、1と72をかけると72ですね。



4も同様に72で割れることを確認します。72÷4=18 4と18を掛けると72です。
このようにして両端の数をかけ算して72になる数を探していくと約数がみつかりやすいですね。全部で12こありました。
(1,2,3,4,6,8,9,12,18,24,36,72)

皆さん、大変よくできました。素晴らしいです。
このように両端から見つけていくと最後の数字は8と9になります。
8と9の間には整数の数字はありません。これで終了です。
一見面倒くさいようですが慣れると暗算でもできますので是非トライしてみてください。
*公約数とは
2つ以上の整数に共通の約数です。
*公約数の指導法
ポイント:素因数分解で最大公約数を見つけ、その数の約数を見つけていく方法。できればこの方法が時間の節約になります。

それでは実際に検討してみましょう。
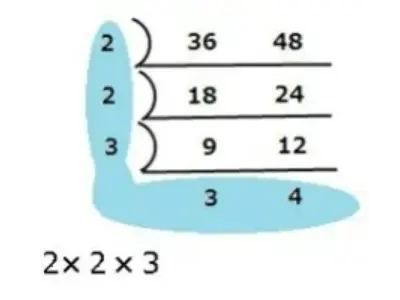
36と48の公約数を因数分解を使って求めなさい。

では検討します。
①36と48は偶数なので2で割りました。また2で割り3で割りました。すると、これ以上割れる数がなくなったのでこれで終了です。
➁縦のブルーの数字3つをかけ算したものが最大公約数で12です。
③12が見つかればその約数が公約数となります。公約数は1、2、3、4、6、12です。

次は素因数分解を使って約数の個数を見つける方法について検討しましょう。
約数の個数の見つけ方
数が小さければ上記の方法で十分なのですが数が大きいと時間がかかりますよね。そこで素因数分解を使った簡単な方法をご紹介します。
例えば256のような数の約数を求めましょうと言われたら大変だなと思いますよね。でも素因数分解をしてみれば簡単にわかるのです。

*108の場合はどうなるかみてみましょう。
108を素因数分解すると2×2×3×3×3になります。
2は2回出てきたので1を足して3こ、3は3回出てきたので1を足して4ことなりました。
これらの数を掛け算すると12です。 答え 12こ

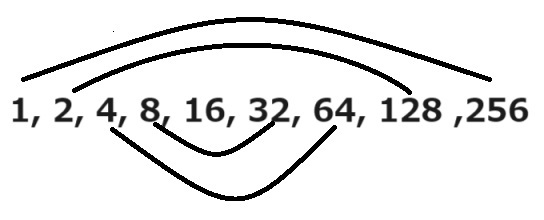
では256から確かめてみましょう。
1番小さい数と1番大きい数をかけ算して256、2で割れるので2と128、4で割れるので4と64,8で割れるので32、両側からつめてきたので間の数は16となりました。合計すると9こです。線でつながっている数字をかけると256になっていますね。

つぎは108の確かめです。
素因数分解だと2×2×3×3×3でした。2が2個で1を足して3、3が3個で1を足して4、これらをかけ算するのでしたね。3×4=12 12個でした。
上記と同様に1,108から始めて2,54と3,36と 4,27そして 6,18最後は 9,12と見つけました。これらの組はすべてかけ算すると108です。よって12ことなりました。
これら2つの数字からもわかりますように素因数分解を使うとこ数に関しては速く処理できます。
3.通分と約分

通分とは2つ以上の分数の分母を公倍数を見つけてそろえることです。
*通分の指導法
ポイント:2つの数、3つの数の公倍数のパーターン練習が必要ですので数字を組み合わせを変えながら行いましょう。最初は倍数をていねいに書きだしてもらい、つぎは慣れてきたら上記のように素因数分解を利用して求めるようにすると良いと思います。慣れてくると頭の中で公倍数が浮かんできます。
例
*2つの数の場合 (12と9)→36 (16と24)→48 (15と20)→60 (12と18)→36
*3つの数の場合 (2と3と5)→30 (4と6と8)→24 (3と4と9)→36 (6と8と9)→72

例:1/3と3/4で通分してみましょう。
①まず、分母の3と4の最初にでてくる公倍数を上記の方法で書き出して見つけなさいと指示します。
➁公倍数は12ですね。1/3の分母3に幾つを掛けたら12になるか質問します。4と答えたら3のわきに×4、分子1のわきに×4と書かせます。それを計算すれば4/12となりますね。
同様に3/4も上と同様にやってもらいます。今度は×3ですね。すると9/12となりました。
③このようにして分母をそろえることを通分だと教えてください。後日、この練習の前には通分とは?の質問から始めましょう。
あるお子様には簡単であっても実行する手順を身に付ける作業だと思ってお子様が簡単だよと言ってもきちんとやらせてください。

約分とは分母と分子を共通な約数で割っていき、これ以上割れなくなるまでの作業です。
*約分の指導法
ポイント:初めに2つの数で公約数の練習をさせてください。つぎに分数で公約数を見つける練習です。
例
(12と18)→(1,2,3,6)
(20と15)→(1,5)
(24と36)→(1,2,3,6, 12)
(18と27)→(1,2,3,9)
(11と55)→(1,11)

*練習問題:5/15と40/24の2問
①5/15は公約数は5ですから分母と分子のわきに÷5と書き込み計算させてください。すると1/3になります。分母と分子が1でしか割れない場合はこれが答えだよと言ってください。
➁40/24などの数字が大きい場合は2などの小さい数字で割っていくのもOKだよ、その代わり何回も割らなければならないよと教えてください。
40/24=20/12=10/6=5/3と3回約分しました。これを基にできるだけ大きい数字で割った方がいいねと実感させます。そこで最大公約数の登場です。
40と24の最大公約数を見つけさせます。できれば練習を重ねて素因数分解をすらすらできるようにしておくほうが良いと思います。そうすると小さな数は約数が頭に浮かび8と答えが出てくようになります。
4.練習問題
①東京駅からある電車が9分ごとに、バスは15分ごとに出ています。午前8時に出発するとつぎに同時に出発する時間は何時何分ですか。また午後1時までには何回同時に出発しますか。午前8時も1回と数えます。
②108,144,180の最大公約数と最小公倍数を求めましょう。
③36とある数の最大公約数は12で最小公倍数は144です。ある数はいくつでしょう。
5.解答
①9と15の最小公倍数は45なので8:00 のつぎは8:45です。このようにして45分ずつ時間を進めていくと9:30、10:15、11:00、11:45、12:30の7回です。 答え7回
②素因数分解で2で2回、3で2回割りますと1番下に3、4、5と数字が並びます。最大公約数(2×2×3×3=36)は36です。最小公倍数は(36×3×4×5=2160)2160です。
③公式を覚えてください。ある数Aとある数Bをかけ算すると最大公約数と最小公倍数をかけたものに等しい。つまりA×B=最大公約数×最小公倍数です。
この式にあてはめます。36×B=12×144 B=12×144÷36 B=48 答え48
6.まとめ
通分や約分がどうも苦手で数字が嫌いになりそうだと感じている児童がおられれば、ご父兄の協力のもと初めはある数字をいくつか提示してその数字の約数、倍数を見つける作業をさせて下さい。
この作業が通分や約分につながっていき、数字に対する感覚が良くなります。
つぎは公約数、公倍数と進んでいきましょう。
さらに、大きい数で3つの公約数は素因数分解を利用して最大公約数を求めてみましょう。
最小公倍数の場合も同様に素因数分解で求めてから2倍、3倍していくと時間もかかりませんし、大きい数でも苦になりません。ぜひ試してみてください。