クリックできる目次
1. 中心角と円周角

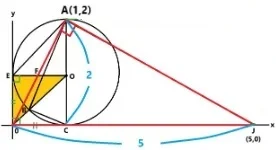
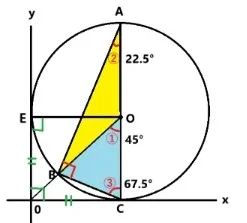
問1. 半径1の円がx軸とy軸に接しています。このとき①➁③の角度を求めてください。


ヒントが3つあります。
- 四角形E0COは正方形です。
- ①と②の関係は中心角と円周角の関係です。
- 三角形OBCは2辺が半径が等しい2等辺三角形です。
2. 1の解説

問1の解説をします。
①の角度は四角形E0COが正方形なのでその対角線であるO0は90°を二等分しています。よって答えは45°です。つぎに➁は弧BCの円周角です。中心角①が45°なのでその半分になりますから答えは22.5°です。最後に③は三角形OBCが二等辺三角形なので180°から45°を引いて2で割ります。すると答えは67.5°になりました。
3. 相似な三角形を探す

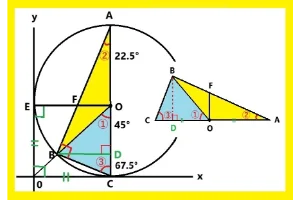
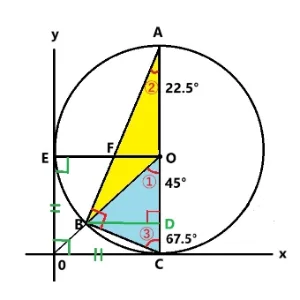
問2. 三角形ABCと相似な三角形を見つけてください。

ヒントは3つです。
- 三角形ABCは直角三角形です。理由は辺ACは直径なので弧ACに対する円周角は90°だからです。
- 直角三角形の相似はその中の直角三角形にあります。
- 共通した角度を探してみましょう。
4. 3の解説

問2の解説をします。
まず三角形ABCの中の直角三角形に注目します。するとすぐに見えるのは三角形AOFと三角形ADBです。これら2つとも直角三角形で共通した角はA➁です。よって直角とA➁が等しい(2角が等しい)ので三角形AOFと三角形ADBは相似ですね。
つぎに三角形BDCを見ると横になっているので縦に起こしました。するとC ③は共通の角、もうひとつは直角(または22.5°)です。2角が等しいので三角形BDCも相似です。
答え 三角形AOF、三角形ADB、三角形BDC
5. 底辺の長さから考えた面積比

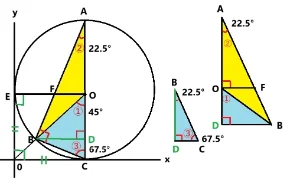
問3. 三角形BCAと三角形BCOの面積比を求めてください。

ヒントが2つあります。
- 三角形BCAを右に90°回転させましょう。
- 底辺の長さに注目しましょう。
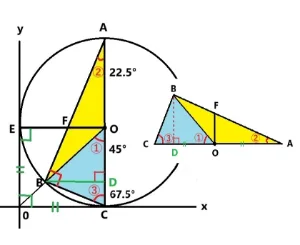

問3の解説です。
右に90°回転させた三角形BCDを見ますと底辺CAと底辺COは直径と半径により2:1であることがわります。また点Bから辺CAに垂線を降ろしました。すると三角形BCAと三角形BCOの高さBDは共通です。よって面積比は底辺の長さの比になりますの2:1です。答え 2:1
6. 平行線と等積変形

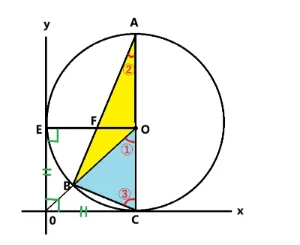
問4. 三角形E0Oと面積が等しい三角形を見つけてください。
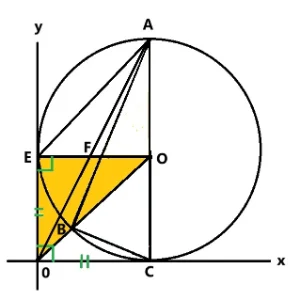

ヒントが3つあります。
- 辺0Oと平行な辺を探しましょう。
- 傾きが同じ直線は平行線です。
- 辺0Oを底辺として高さが等しい三角形を探しましょう。
7. 平行線と等積変形の解説その1

問4の解説その1です。
三角形E0Oの辺0Oを底辺とすると高さは垂線EGです。辺AEと辺O0は共に傾きが1になっているので平行です。もう一つの三角形は辺0Oを底辺としますと高さが等しくなければいけません。
よって平行線をOからHまで延長しますとAからHに垂線が引けます。これで高さEG=高さAHになりました。したがって三角形E0Oと三角形A0Oは底辺と高さが等しいことがわかりましたので面積は同じです。
答え 三角形A0O
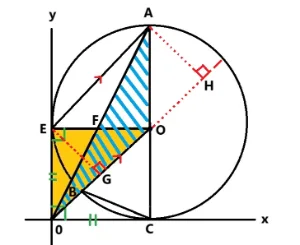

解説その2があります。
今度は図を左に90°回転させてください。すると三角形E0Oの底辺が辺E0となり高さがOEとなります。もう一つ底辺と高さが等しい三角形がありました。高さIA=高さEOをもつ三角形です。つまり三角形AE0です。
このように底辺の共通を探し平行線から高さが等しいことを見ていけば面積が同じ三角形が見つかります。
答え 三角形AE0
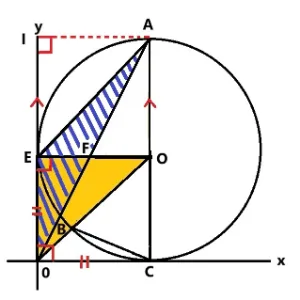
8. 直線の式から面積を考える

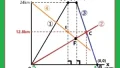
問5. 半径1の円はx軸、y軸に接しています。このとき直線A0に対して垂直に交わる直線AJの直線の式を求めてください。またそのときの三角形A0Jの面積を求めましょう。
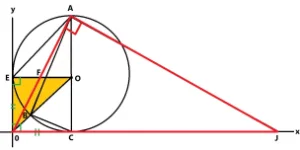

ヒントが2つあります。
- 2直線が垂直で交わるときは傾き×傾き=-1になります。
- 直線AOの傾きを求めてから公式にあてはめましょう。
9. 直線の式から面積を考えるの解説

問5の解説をします。
直線A0の直線の式はy=2xなので傾き×傾き=-1にあてはめると2×傾き=-1になります。すると傾き=-1/2と出てきますのでy=-1/2x+bとおきます。この式にA(1,2)を代入しますとb=5/2と出ました。よって直線AJの式はy=-1/2x+5/2になります。
答え y=-1/2x+5/2
続いて三角形A0Jの面積の解説です。
まずy=-1/2x+5/2の式にy=0を代入するとx=5なのでJの座標は(5,0)です。よって三角形A0Jの面積は底辺0Jは5、高さACは2なので5×2÷2=5となります。 答え 5