1.半径をxとして辺の長さを決めていく方法

①6cm、8cm、10cmの直角三角形があります。その中に内接円があります。内接円の半径を求めましょう。
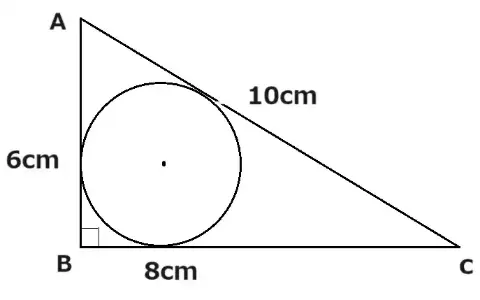

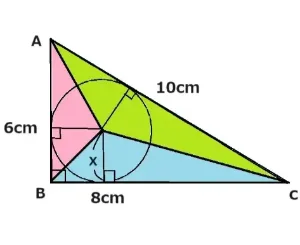
まず初めに内接円について解説します。内接円はこの場合だと三角形の3辺の内側に接している円のことです。辺AB、辺BC、辺CA上で円が接しています。
つぎは点Aからの2つの接点までの距離は等しくて、また点Bからの2つの接点までの距離は等しい。
そして最後に点Cからの2つの接点までの距離は等しい。これらのことを利用して問題を解いていきます。図では3色で使い分けをしました。


なぜ同じ長さになるのですか。

オレンジ色で色を付けた2つの三角形の形、大きさが同じだからです。これを合同な三角形と言います。
また注意しなくてはいけないことが1つあります。それは接線とそこから中心に向かう線(半径)のなす角度は常に90°です。これらの理由で点Aから2つの接点までの長さが等しくなるのです。
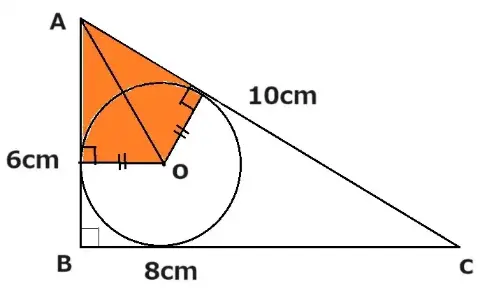

覚えることがたくさんありますね。

それではBD(半径)をXと決めるとDCの長さが8-X と決まりますね。するとCEの長さはどうなりますか。
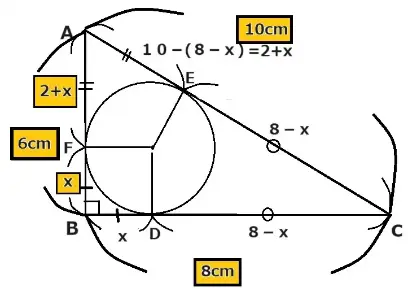

点Cから点Dまでと点Cから点Eまでは同じだと教わったので8-Xです。

そうです。つぎが大変です。辺ACは10cmなので辺AEの長さは10ー(8-X)になります。
これを計算すると10-8+X=2+Xです。小学生には計算は大変でもAEとAFの長さが等しいとわかればOKです。
そうすると、AFの長さはどんなふうに表されますか。

はい、AEと同じ長さなので2+Xです。

FBは最初に決めたBD(半径)と同じ長さなのでXです。
ユウ君、図の辺ABをよく見てください。上の2+Xと下のXを合せると6cmですね。
これで式を作ると2+X+X=6になります。計算すると2X=6-2 2X=4 X=2となりす。 答え 2cm
2.三角形の面積から半径を求める

今度は三角形を3つの三角形に分けて、それぞれの面積をXを使って表しその合計の式を作っていきます。
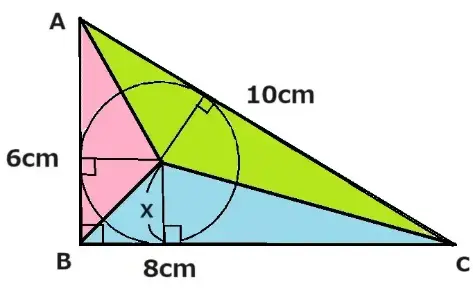

ピンクと青と緑の部分の3つですね。

では3つの三角形のピンクの部分の面積から求めていきましょう。高さは円の半径なのでXで表せます。

底辺は6cmで高さはXなので6× X ÷2=3× X です。

3× X の×は省略していいですよ。すると3Xですね。残り2つも求めましょう。

はい。青の部分は4Xで緑の部分は5Xです。

その3つを足し算すると3X+4X+5X=12Xになります。では直角三角形の面積を求めてください。

はい。8×6÷2=24で24㎠になりました。

そうしたら先ほど求めた12Xと24を=でつなげます。すると12X=24になり、X=2となり答えは2cmです。

12Xは12×Xのことでしたよね。だから割り算して答えを求めたのですね。

その通りです。2つの解き方面白かったでしょう。

はい、とっても。ますます算数、数学が面白くてわくわくしてきました。
3.内接円に関する角度と長さの練習問題

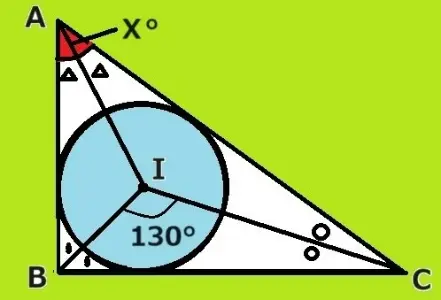
内接円の内心に関する角度の問題です。
∠BICが130°のとき∠BACを求めましょう。
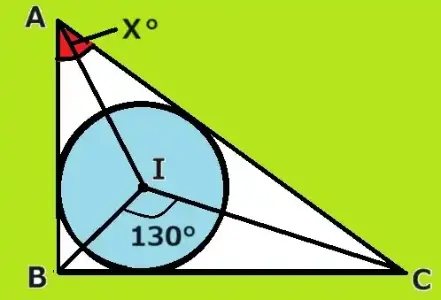

では解説です。
三角形の内心は頂点から角の二等分線を引いて交わったところです。それゆえ△IBCに着目しますと残りの底角2つは50°です。
つぎに△ABCに目を移しますと底角2つで2倍の100°になりますので求める∠BACは80°になります。答え 80°

次は内接円に関する辺の長さについてです。
辺ABの長さを求めましょう。
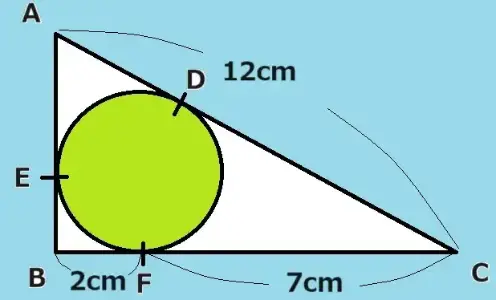

では解説です。
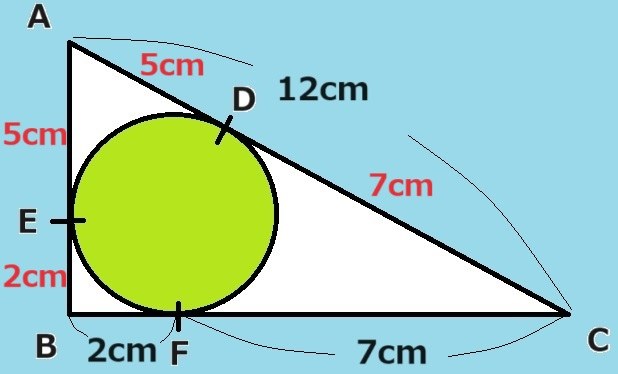
まず最初に頂点Cからみていきましょう。つぎにCF=CDなのでCD=7cmです。つづいてDAの長さは12-7=5で5cmです。そしてAD=AEなのでAEの長さは5cmです。
残りのEBの長さはBFと等しいので2cmです。最後にこれら2つをたして7cmとなります。 答え 7cm
4.まとめ

解き方のまとめです。
- 最初の解き方はある頂点から円の接線を2本引くと接点までの距離は等しいという定理を使いました。これは三角形の合同を使って証明できます。
- つぎは三角形を3つにわけて内接円の半径が等しいことを利用した解き方です。
- 角度については各頂点から角度を2等分した直線が内心となることを利用した問題です。