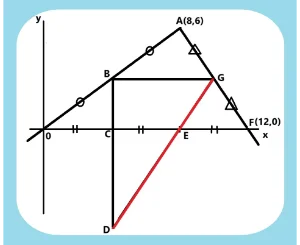
1.直線の式を求める

問1.グラフを見て直線AFの式を求めましょう。
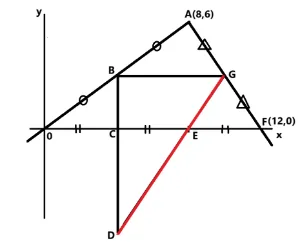

これから解説をします。
2点(8,6)と(12,0)をy=ax+bに代入して連立方程式で解きます。まず6=8a+b、0=12a+bの式を作りこれを解きますとa=-3/2、b=18となります。 答え y=-3/2x+18
2.辺の長さを求める

問2.三角形A0FのB点、G点は各辺の中点です。またC点,E点は辺0Fの3等分点です。まず辺BGの長さを求めましょう。そのあとA点からE点に向かって垂線を引きます。辺BGと交わったところをHとします。そのときの線分BHの長さと線分HG長さを求めましょう。
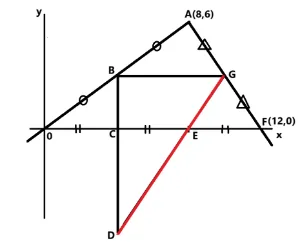

2つのヒントがあります。
- 辺A0の中点がB、辺AFの中点がGなので三角形A0Fからみたときの辺BGは中点連結定理により辺0Fの半分です。
- 点C、点Eは3等分点ですから線分CEの長さがでます。
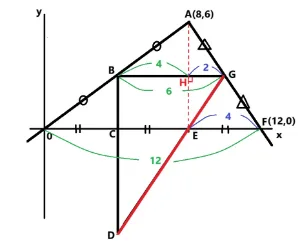

解説をします。
中点連結の定理によりBGは0Fの半分の長さなので6です。 答え 6
AからEに線を引きますとEの座標は(8,0)なので垂線となります。よって辺BGと垂直に交わったHによりBH=CEとなるので線分BH=4です。そして線分HGは6から4を引きましたので2です。 答え 線分BH=4,線分HG=2
3.面積比を求めるその1

問3.三角形ABGと三角形A0Fの面積比を求めましょう。また台形B0FGと三角形A0Fの面積比を求めましょう。
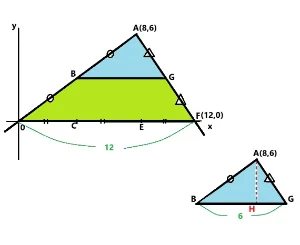

ヒントです。
相似な図形は対応する辺を比べて辺の長さを2乗すると面積比になります。


解説を行います。
三角形ABGと三角形A0Fの底辺を比べると6と12です。つまり相似比は1:2になるので面積比はその2乗の比になりますので1:4です。 答え 1:4
台形B0FGは三角形A0Fから三角形ABGを引いたことにより4-1=3です。また三角形A0Fは4なので3:4となりました。 答え 3:4
4.面積比を求めるその2

問4.三角形AEFと三角形AHGの面積比を求めましょう。また三角形AHGと三角形A0Fの面積比を求めましょう。
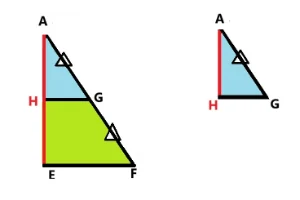

三角形AEFと三角形AHGの面積比の解説です。
三角形AEFと三角形AHGは2:1の相似形なので2乗をすると4:1になります。 答え 4:1
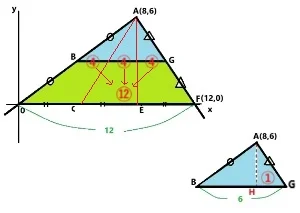

三角形AHGと三角形A0Fの面積比の解説です。
三角形A0Fは三角形AEFの3倍です。したがって三角形A0Fは12です。三角形AHGは1なので1:12になります。答え 1:12
5.面積比を求めるその3

問5. 三角形HEGと三角形BDGの面積比を求めましょう。
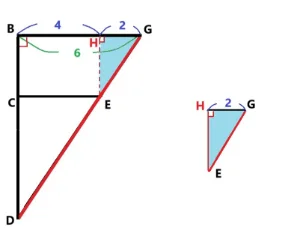

解説です。
三角形HEGと三角形BDGは相似な三角形です。問2で求めたように線分HG=2、辺BG=4+2=6なので線分HG:辺BG=2:6=1:3です。よって面積比は2乗の比なので1:9です。 答え 1:9
6.面積を求めるその4

問6. 三角形A0Fと三角形BDGの面積比を求めましょう。
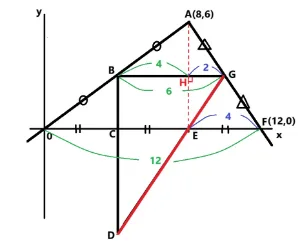

まずはヒントから。
- 三角形A0Fは座標から底辺と高さがわかります。
- 三角形BDGは問2より高さAE=3とわかりましたので線分BC=3です。
- 三角形CDEと三角形BDGの相似比を使います。
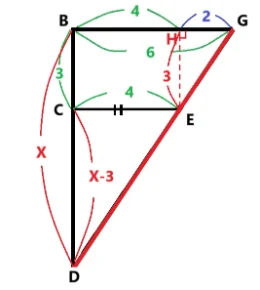

解説をします。
辺BDをXとすると辺BC=3なのでCD=X-3とおけます。相似は三角形に注目すればX:X-3=6:4になります。これをすすめますと6(X-3)=4X 解きますとX=9
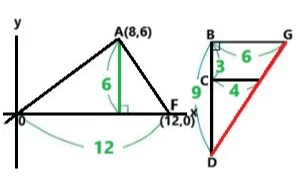

続いてそれぞれの面積を求める解説をします。
三角形A0Fの面積は12×6÷2=36、三角形BDGの面積は6×9÷2=27
よって36:27を9で割ると4:3になります。 答え 4:3
7.直線の式を求める

問7.点Gと点Dを通る直線の式を求めましょう。

ヒントです。
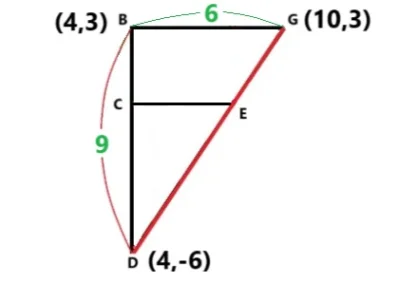
Bの座標は辺AOの中点なので(4,3)右に6進んだところが点Gなので(10,3)で点Bから下へ9降りたところが点Dなので(4,-6)となります。

それでは続いて解説です。
点の座標をy=ax+bに代入しますと3=10a+bと-6=4a+bの2つの式ができました。これを連立方程式で解きます。するとa=3/2 b=-12となりました。これをy=ax+bに代入しますとy=3/2x-12です。答え y=3/2x-12