1. グラフから直線の式を求める
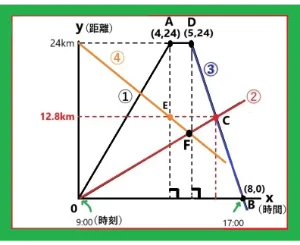
Aさん①はBさん➁と同時にO地点を出発しました。Aさんは24kmの地点で少し休憩して17:00にO地点に戻りました。Bさんは時速2kmでそのまま歩き続けました。

問1.グラフを見て①の直線の式を求めましょう。
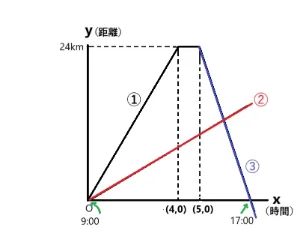

解説をします。
①のグラフから4時間かけて24km進んだことがわかりますので傾きはy÷xです。したがって24÷4=6となり、y=axの式のaに6を当てはめてy=6xとなります。 答え y=6x
2. 帰りの式を求める
Aさんは24km地点で1時間ほど休憩してO地点に17:00に戻りました。

問2. Aさん③のグラフの式を求めましょう。
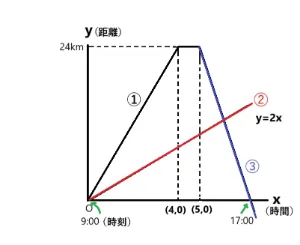

解説をします。
Aさんの休憩後の座標は(5,24)で到着した時は出発から8時間後ですので(8,0)で表すことができます。つまり3時間かけて24km戻ったと考えられます。傾きは右下がりなので-y÷xになります。したがって-24÷3=-8となり、y=ax+bの式のaに-8を当てはめてy=-8x+bとなります。この後切片bを求めるためにy=-8x+bの式に結果の出しやすい(8,0)を代入するとb=64となりました。よって式はy=-8x+64です。 答え y=-8x+64
別解があります。
2点の座標がわかった場合、y=ax+bにそれぞれの座標(5,24)と(8,0)を当てはめます。すると24=5a+b、0=8a+bとなります。この2つの式を連立方程式で解くとa=-8、b=64となります。よって式は上と同様にy=-8x+64となります。 答え y=-8x+64
3. 出会いの式を求める

問3. Aさん③とBさん➁はO地点から何kmの地点で何時に出会いましたか。
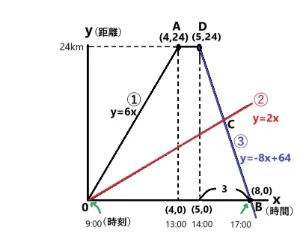

ヒントがあります。
- Bさん②は時速2kmなのでy=2xです。Aさん③は上でy=-8x+64となりました。
- これらを連立方程式で解きます。
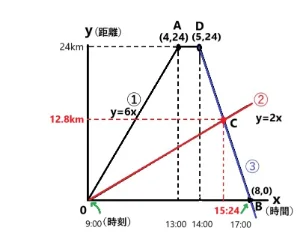

今度は解説です。
Bさん②は時速2kmなのでy=2xです。Aさん③は上でy=-8x+64となりました。これらを連立方程式で解きますとx=32/5,y=64/5です。xは時間なので6と2/5時間を分に直しますと6時間24分です。これを時刻に変えますと9:00時出発から6時間24分進んだことになるので15時24分に出会ったことがわかります。y=64/5は64÷5を計算しますと12.8kmになります。
答え O地点から12.8kmのところで15時24分に出会った
4. 四角形の面積を求める

問4.四角形A0CDの面積を求めましょう。
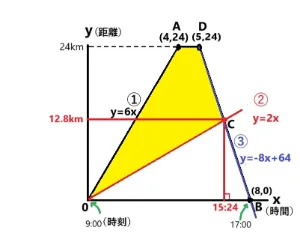

ヒントがあります。
- 台形の面積の公式(上底+下底)×高さ÷2を使います。
- 台形の面積から三角形の面積を引き算します。

次は解説です。
台形の面積は(1+8)×24÷2=108です。この面積から三角形C0Bの面積を引きます。三角形の面積は8×12.8÷2=51.2です。108-51.2=56.8 これが四角形A0CDの面積です。 答え 56.8 *単位がない問題の場合は㎠などの単位は答えに付けません。
5.出会いの式を求めるその2

問5.Cさん④はAさん①と同じ9:00に24kmの地点から戻りました。途中E地点を通っています。何時何分にそしてO地点から何kmのところでBさん➁と出会うでしょうか。
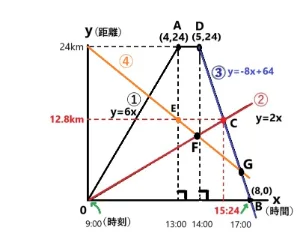

ヒントが3つあります。
- 24km地点とE地点の座標からCさん④の座標を求めましょう。
- 求めたらBさん②の式で連立方程式を作り解きましょう。
- 同様にAさん③の式で連立方程式を作り解きましょう。

解説をします。
Cさん④の座標は出発点(0,24)とE地点(4,12.8)です。これらをy=ax+bの式に代入すると24=b 12.8=4a+24になるのでこれを解くとa=-2.8 分数に直すとa=-14/5になりました。
よってCさん④の式はy=-14/5x+24です。Bさん②はy=2xなのでこれらの式を連立方程式で解きます。するとx=5,y=10となりました。xは時間なので5時間後つまり9時から5時間後で14時です。yはO地点から何kmの地点かを示すので10km離れたところとなります。
答え 14時にO地点から10km離れたところ