ご父兄にとってひし形の指導はたいへんです。しかしながら、基礎となるひし形の性質をマスターすれば、お子さまの図形に対する興味がわき、図形へのステップアップとなるでしょう。
またさらに、定規使いも丁寧に進めていけば、垂線、平行線、三角形、平行四辺形さらに円まで自由自在に描けるようになります。
ひし形指導法でお困りのご父兄は以下をご覧ください。対象は4、5年生です。
クリックできる目次
1.ひし形の定義と性質

ひし形の特徴を言える人いますか。

はい、4つの辺の長さはすべて等しいです。
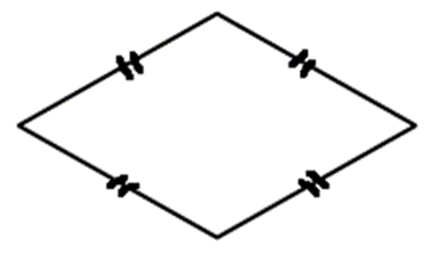

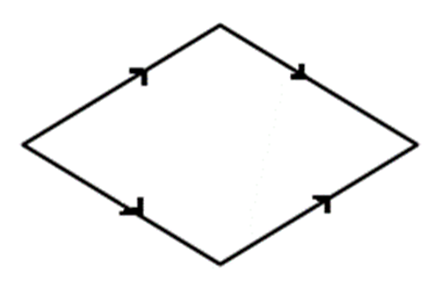
はい、向かい合った辺は平行です。平行四辺形の仲間といえます。

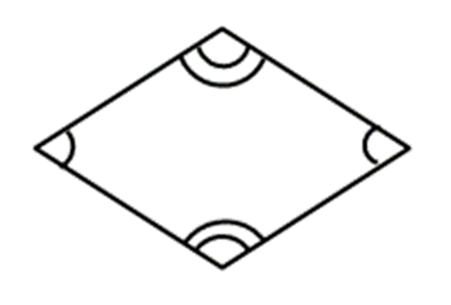
はい、向かい合った角の大きさは等しいです。

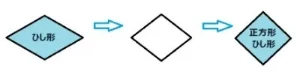
1つの角度が90°の場合、ひし形は正方形の仲間でもあります。

2つの対角線は垂直(90°)に交わります。

このように5つの性質を挙げてもらいました。これらをみなさんがすらすら言えるようにしましょう。マスターしたかどうか常に確認してください。
- 4つの辺の長さはすべて等しい
- 向かい合った辺は平行である (平行四辺形の仲間)
- 向かい合った角の大きさは等しい
- ひし形は正方形の仲間でもある(1つの角度が90°の場合)
- 2つの対角線は垂直(90°)に交わる
2.3通りのひし形の描き方

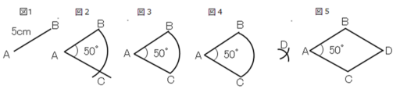
次はひし形の描き方です。三つのがありますが説明できますか。

はい、まず長さ、角度を設定して描く場合です。
*図1:5cmの直線ABを引きます。
*図2:点Aから2.5cmのところに分度器をセットして50°を測る印を付けたら点Aから印に線を引きます。点Aにコンパスの針を刺し、点Bからコンパスをまわします。交わったところを点Cとします。
*図3:はみ出た部分を消します。
*図4:点Bにコンパスの針を刺し印を付け、同様にして点Cに針を刺し交差するように印を付けます。
*図5:点B、点Cから交差した点に直線を引き、交差した点を点Dとして完成です。

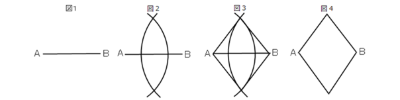
はい、長さ、角度の設定なしで描く場合があります。
*図1:直線ABを引きます。
*図2:点Aにコンパスの針を刺しコンパスをまわす。同様に点Bにコンパスの針を刺しコンパスをまわします。
*図3:交わったところに点A、点Bから線を引きます。
*図4:中の線を消して完成です。

はい、長方形から描くことも考えられます。
*図1:簡単に書く場合はまず縦6cm、横8cmくらいの長方形を描きます。

*図2:各辺の真ん中に印を付けます。そこを線で結ぶと中にひし形ができます。
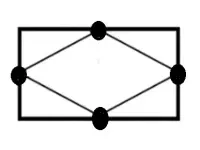
*図3:長方形を消してひし形が完成です。

3つの例を挙げてもらいました。これら3つはそれぞれ特徴のある書き方ですので覚えるまで何回も練習してください。まとめますと以下の3つです。
- 例1は辺の長さ、角度を指定してあります。
- 例2はABの長さ(自由)、つまり対角線からコンパスで描く方法です。
- 例3は適当な大きさの長方形の中点から描く方法です。
3.ひし形はなぜ正方形の仲間といえるのか

今度は対角線から見たひし形の性質をけんとうしましょう。
対角線によって2等分できる図形にはひし形、正方形(この2つは仲間)、この2つのほかにも2等分できる図形は正六角形や正八角形などがあります。
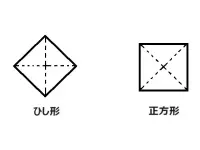

対角線によって2等分できない図形もあります。下図をご覧ください。
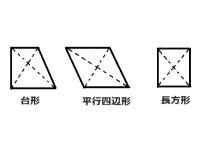

今度は対称な図形から見たひし形の性質について見ていきましょう。
*線対称(折ってみて重なる)の図形:ひし形、正方形、長方形
*点対称(回しても元の形と同じ)の図形:ひし形、正方形、長方形、平行四辺形
これらの点からひし形と正方形の共通点が見いだされました。よってひし形は正方形の仲間であることがわかりました。
ひし形にもう1つの条件を加えるとひし形=正方形になります。その条件とはひし形のそれぞれの角度が90°であることです。
4.ひし形の角度について
お母さんとサラちゃんの会話例

左側の角度が40°のとき中央の上の角度を求めましょう。


左側の角度が40°であれば右側も40°です。

よくできました。では対角線を1本引きましょう。三角形はいくつできましたか。

2つできました。

三角形の内角の和は180°ですね。四角形の内角の和は?

2つできたから360°です。すると、360‐40x2で残りの角度は280°になります。上側と下側2つで280°なので2で割ります。答えは140°です。

そうです。四角形以上の多角形に対角線を1本引くと対角線+1の数の三角形ができるの。
これはとても大切ですね。ぜひ、覚えておきましょう。
つぎにもう一つの考え方を教えてあげますね、サラちゃん。
それは三角形に注目します。上側の三角形の底角はひし形の40°の半分の20°です。底角は両側にあるので40°ですね。
すると、残りの角度は180-40=140となるのでこのようにしても求められますね。

なるほど。いろいろな考え方があるのですね。勉強になります。

角度の問題をまとめます。これらをおさえておけば角度の問題は解決です。
- ひし形は向かい合う角が等しい。
- 対角線が垂直(90°)に交わる。
- 4つの辺は等しい。
- それからもう一つ、算数や数学は公式から解こうとするのではなく、どうしたら解けるのだろうかを考えるともっと力がつきますよ。
5.ひし形の面積、なぜ2でわるのか

長方形からひし形を書く方法を上記で説明しました。このことを利用して面積について考えていきましょう。
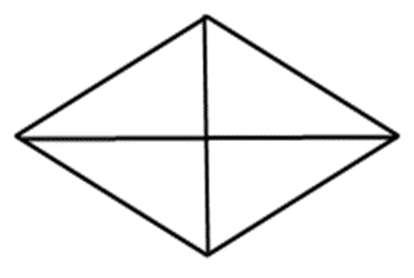
初めに、ひし形に2本の対角線を引くと、ひし形の中に4つの三角形と外側に4つの三角形、合計8つの三角形ができました。
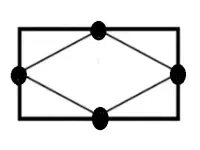
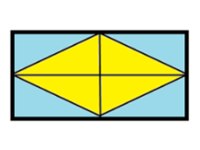

すると、長方形は8個の合同の三角形でできていることがわかりました。
よって、ひし形は三角形の数が4個なので長方形の半分であることが理解できます。
結果として、ひし形の面積に÷2が付く理由がそこにあったわけです。
したがって、次の公式が導かれました。
*ひし形の面積=対角線(縦)x対角線(横)÷2
練習問題
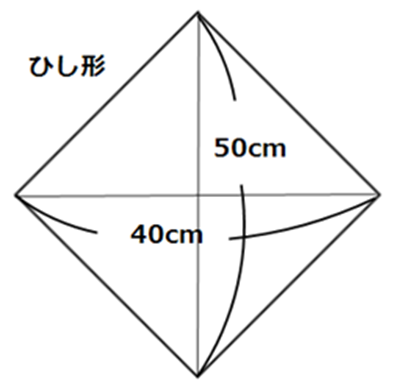
お母さんとサラちゃんの会話

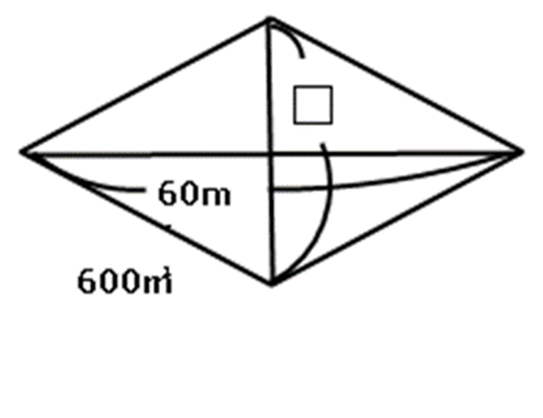
面積や高さを求めましょう。

はい。ひし形ですから公式は対角線×対角線÷2です。だから40×50÷2=1000 答えは1000㎠です。
もう一つはまず式を作ります。60×□÷2=600です。式に÷2があるので半分の600になっています。もし÷2がなかったら1200のはずです。
すると、式は60×□=1200になります。□=1200÷60 □=20 答えは20mです。

そうです。順序立てて説明できるようになりました。すばらしいことです。

よかった、勉強がんばって。これからもっとがんばります、お母さん。
6.対角線から多角形の内角の和についての考察

ひし形で対角線という言葉が出てきましたので、さらに深掘りする意味で多角形の内角の和について考えていきたいと思います
サラちゃんとお母さんの会話

多角形の角度の問題に踏み込む場合、対角線を引くようにすると良いと思います。
三角形がいくつできるか分かるのでこのことが問題を解く手がかりになります。下の図をよく見てみましょう。
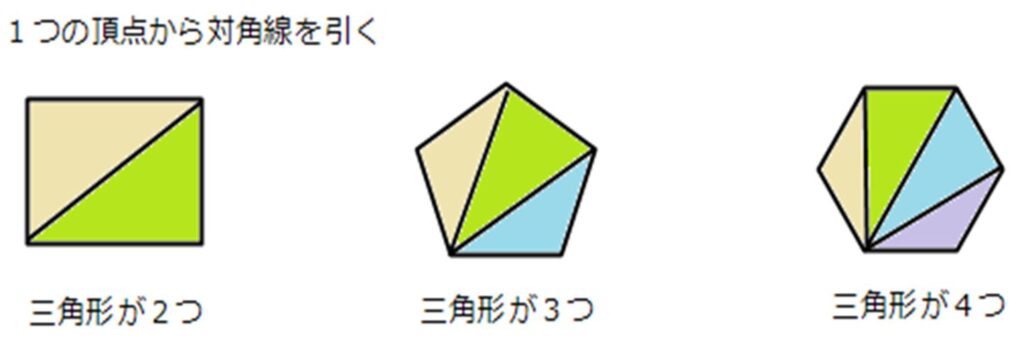

このように対角線を引くことで三角形の数がわかりますね。
対角線が1本だと三角形が2つ、対角線が2本で三角形が3つ、さらに対角線が3本で三角形が4つというように対角線プラス1が三角形の数になります。
そしてさらに、上の3つの多角形から次のようなことも分かりました。
四角形は三角形が2つ、五角形は三角形が3つ、六角形は三角形が4つできています。
このことから多角形-2=三角形の数が導かれました。これを覚えておくと内角の和を求めるときは便利ですね。

この図で対角線の引き方を理解しました。また、内角の和は三角形の数×180°で考えればよいこともわかりました。おかあさん、いつもありがとう。

では、いくつか内角の和を求めてみましょう。四角形、五角形、六角形の内角の和です。

四角形は三角形が2つだから 内角の和は180×2=360°です。
五角形は三角形が3つだから 内角の和は180×3=540°です。
六角形は三角形が4つだから 内角の和は180×4=720°です。

よくできました。
対角線の数や三角形の数に注目すると公式を覚えていなくても解けますよ。
- 対角線 +1=三角形の数
- 多角形 -2=三角形の数
- 内角の和=三角形の数×180°

なるほど、公式は図の性質をつかめばわかってくるものですね。
7.まとめ
ひし形を理解するには正方形や平行四辺形と比較をするとよりいっそうわかりやすいです。
最初に比較検討して、平行四辺形、ひし形の共通する点、違う点をしっかりと理解させてください。
そして次に、理解したか否かの判断の基準は図形を描けること、性質を言えること、違いはどこかの3点をよく見極めることだと思います。
さらに、台形や三角形の性質などほかの図形にまで目を向けると幅が広がりますね。
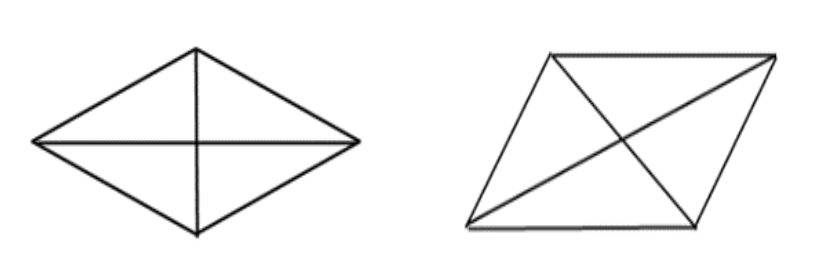
共通する点:ひし形も平行四辺形も2組の辺が平行です。さらに向かい合う角度は等しいです。対角線はどちらも2本引けます。また、ひし形を少し傾ければ平行四辺形になります。
違う点:ひし形は4つの辺が同じ長さですが平行四辺形は4つの辺が同じ長さでない場合があります。ひし形は対角線が垂直に交わりますが平行四辺形は違います。


