小4では各単元の基礎から発展へとつながるものをしっかりとマスターしておいてほしいです。そうすれば今後ずっと楽しくお勉強が進められると思います。
今回もご父兄による正方形とその中の正三角形の見極めのポイントをいくつかご紹介します。ご父兄のご協力をお願いします。
読んでほしい対象者:ご家庭で4年生に図形をどう教えたらよいのかコツを知りたいご父兄方々です。また、等積変形に興味がある4年生から6年生さらに高校受験生にも有効です。
クリックできる目次
1. 正方形と正三角形

正方形の中に三角形が4つあります。左の二等辺三角形の角度X、Yについて考えて見ましょう。
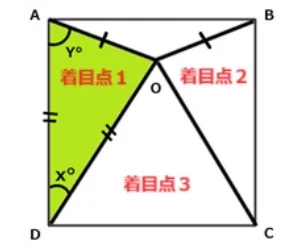

どんなところに着目したら良いでしょうか。

まず、二等辺三角形ADOに着目します。(着目点1)正方形の1辺ADは辺ODと同じ長さです。
つぎに右側の三角形BCOは二等辺三角形ADOと合同(形も大きさも同じ)です。(着目点2)
したがって辺OCは正方形の1辺と同じ長さです。
よってOD=OC=DCとなり、真ん中の三角形ODCは正三角形で一つの角度は60°になります。(着目点3)
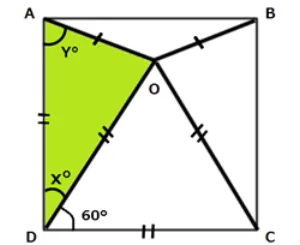

ここからは大丈夫です。説明させてください。
正方形は4つの角度がどこも90°です。
すると、Xは90-60=30となります。よってXは30°です。
残りの2つの角、∠DAOと∠DOAは180-30=150となります。
二等辺三角形は底角が2つあるので1つは150÷2=75です。よってYは75°です。

まとめますとまず正方形、つぎに左側の二等辺三角形と右側の二等辺三角形です。
この3つの図形から三角形ODCが正三角形であることを導きます。

つぎは1辺が10cmの正方形の中にある緑の部分の面積について考えて見ましょう。
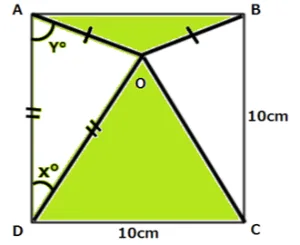

それぞれの三角形に高さがないので難しいと思うのですが。

いいえ、難しくありませんよ。
2つの三角形のそれぞれの高さが出ていませんが図のように辺ABから辺DCに向かって垂線を引けば2つ分の三角形の高さになります。
したがって高さは10cmとなります。
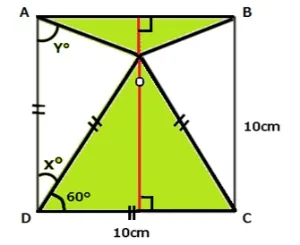
*底辺の長さが同じ三角形は高さを2つ分合わせて1つ分の三角形として計算できます。

なるほど、それでは簡単にできます。
底辺10cmと2つの三角形の高さを合せると10cmになるので式は10×10÷2です。
よって答えは50㎠です。

つづいて三角形BCOの面積について考えてみましょう。

先ほどの三角形2つ分の面積が50㎠だったので残りは50㎠です。
残り2つの三角形は合同(2つがぴったりと重なる)なので50÷2です。よって答えは25㎠です。
別解もあります。
図のように2つの三角形は合同なので三角形BCOも三角形ADOも三角形の高さは5cmとなります。
よって10×5÷2で求まります。よって答えは25㎠
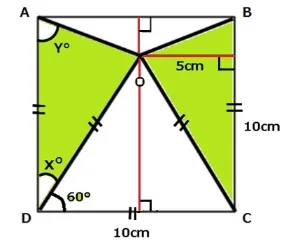
2.三角形の等積変形

問題をがらりと変えてみます。
等積変形の問題です。等積変形というフレーズを聞いたことがありますか。

聞いたことがあるようなないような?はっきりしません。

面積を変えないで三角形の形を変えることを等積変形といいます。
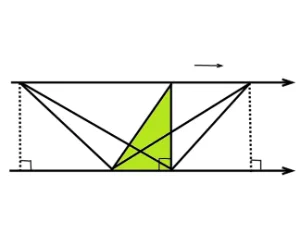

まず真ん中の緑の三角形に着目してください。
そして頂点を右に移動させました。見た目では面積が同じか分かりませんが底辺の位置は変わっていません。そして高さも同じです。
このようにして底辺、高さと順に見ていけば金色の面積が同じであることがはっきりします。
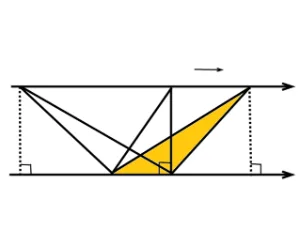

つぎに頂点を左に移動させました。ピンクの細い形の三角形ですが底辺、高さともに同じですから面積は同じですね。

*面積が同じかそうでないかの判断は見た目ではなく底辺と高さが同じであるかしっかりと見極めましょう。
3.練習問題
三角形ABOを等積変形した三角形はどれでしょう。
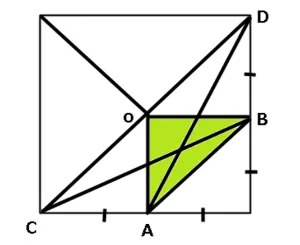
ヒント➀辺ABを底辺とみてください 。
ヒント➁辺ABと辺CDは平行です。
ヒント③辺ABを底辺として辺CD上にある垂直になる点を探してください。そこが三角形の高さです。
ヒント④Aから辺CDへの垂線の長さとBから辺CDへの垂線の長さは等しいです。
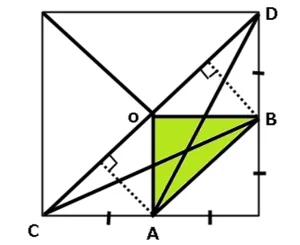
*三角形ABCの底辺と高さをもう少しわかり易く図解しました。
底辺は辺ABで高さは垂線CEです。
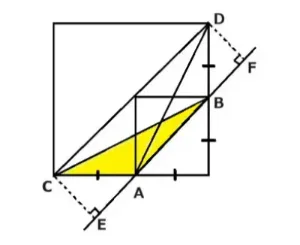
*三角形ABDの底辺と高さをもう少しわかり易く図解しました。
底辺は辺ABで高さは垂線DFです。
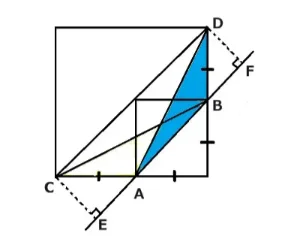
よってこの2つの三角形ABCと三角形ABDは三角形ABOと底辺が共通で高さが等しいので面積が等しくなります。
答えは三角形ABCと三角形ABDの2つです。
4.まとめ
ひととおり平面図形をマスターしたら立体に関することを学習されると良いと思います。
なぜなら中学生になると、角柱、角錐、円柱そして円錐の体積、表面積などの複雑なものを学習するからです。
さらに、これらの立体の中の相似の問題(中3)や三平方の定理のを使った長さなどの高校入試問題がオンパレード状態だからです。
今から立体を頭の中で描ける準備をされてはいかがでしょうか。