1.道のり、速さ、時間の関係をグラフで読み取る

道のりと時間の関係についてグラフで見ていきましょう。
図をみてどんなことがわかりますか。

はい、いくつか分かることがあります。
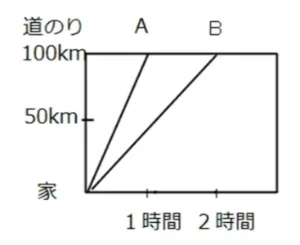
*A君、B君ともに家から同時に100km離れた地点に向かいました。
*A君は1時間で100kmの地点に着いたので時速100kmです。
*B君は2時間で100kmの地点に着いたので時速50kmです。
*傾きが大きい直線ほど速くて逆に傾きが緩やかなほどおそいことが分かります。

するどい観察眼ですね。すばらしいです。

ありがとうございます。

次のグラフはどうでしょう。

グラフで分かることもいくつかあります。
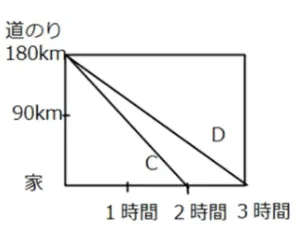
*C君,D君ともに同時に180kmの地点から帰宅しました。
*C君は2時間で180kmの地点から帰宅したので時速90kmです。
*D君は3時間で180kmの地点から帰宅したので時速60kmです。
*帰宅のときも同様に緩やかな直線ほど速度がおそいことが分かります。
2. 相似形を利用したグラフの問題1

たいへんよくできました。次の問題です。相似形を利用したグラフから家から出会いまでの時間と家からの距離を求めましょう。
図から分かることは何ですか。
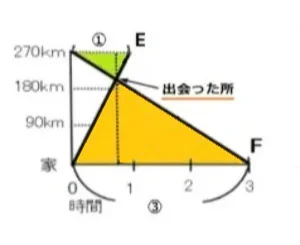

*E君は家から270km離れた地点に向かいました。
*E君は1時間で270kmの地点に着いたので時速270kmです。
*F君は270kmの地点から帰宅の途につきました。
*F君は3時間で270km進んだので時速90kmです。
*E君とF君は途中何分かたって、また何キロメートルか進んだところで出会いました。
*傾きが大きい直線ほど速く、逆に傾きが緩やかなほど遅いことが分かります。

たくさん分かりましたね。もう少しわかることがあります。
速さが1:3だとかかる時間は3:1ですね。この関係を反比例といいます。これは6年生で学習します。

はい。もっと頑張ります。

問題の解法を図から考えて行きましょう。
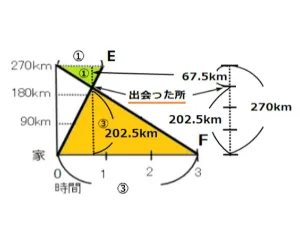

まず、1:3の相似の三角形に着目します。各辺が1:3だけではなく高さも1:3になっています。
すると、270kmが1:3に分けられます。全部で4つに分けることができます。
270÷4=67.5 よって1つの目盛りは(270÷4=67.5) 67.5kmになります。
出会った所は3つ目の目盛りですから67.5×3=202.5 つまり、E君は家から202.5kmの地点で出会ったことになります。 答え202.5km

1:3が4つの目盛りに分けられることが理解できれば易しいです。

そうですね。次は出会いまでの時間について考えてみましょう。
出会った時間は公式の道のり÷速さで求まります。202.5÷270=0.75(時間)0.75×60=45(分)
もう一つの解法があります。
E君は270km/時の速さ(60分で270km移動する)で目盛りの4分の3の所まで進み出会っていますので60分に4分の3を掛けると答えがでます。
60×3/4=45(分) 答え45分

いろいろな考え方があっておもしろいです。グラフの問題は好きになりそうです。
3.相似形を利用したグラフの問題2

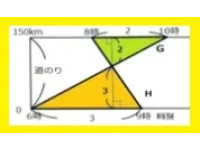
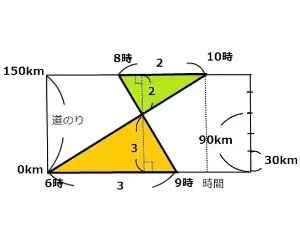
G君が0地点から150km離れた所に向かいました。H君は逆に150km地点から0地点に向かいました。図5を参考にしてH君がG君と出会うのは0地点から何キロメートルのところですか、また時刻は何時何分ですか。図5からわかることはどんなことですか。
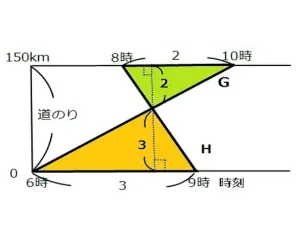

*G君は6時に0地点から150km離れた地点に向かいました。
*G君は4時間で150kmの地点に着いたので時速37.5kmです。
*H君は150kmの地点から2時間おくれて0地点向かいました。
*H君は1時間で150km進んだので時速150kmです。
*G君とH君は途中何分かたって、また何キロメートルか進んだところで出会いました。
*傾きが大きい直線ほど速く、逆に傾きが緩やかなほど遅いです。

問題の解法を図から考えて行きましょう。
まず、2:3の相似の三角形に着目します。各辺が2:3だけではなく高さも2:3になっています。
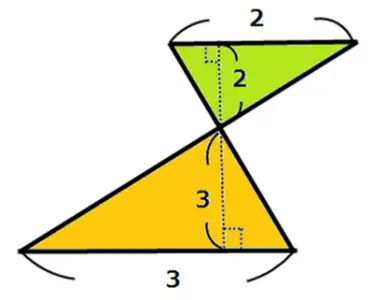

すると、150kmが2:3に分けられます。
全部で5つに分けることができます。1目盛りは30kmですから3つ分で90kmです。 答え 0地点から90kmのところ

今度は150㎞を2:3に分けられることがポイントですね。

そうです。でもね、時刻を求めるには横軸も使います。
そして、大小の三角形を作って相似比で解きます。下の2つの図は1つの図をわかり易く分けたものです。
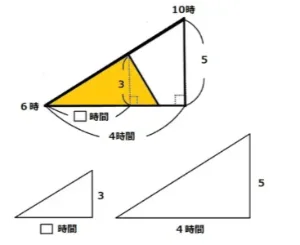

左の図の横軸は出会うまでの時間を□としました。右の図は150km進むのに4時間を意味しています。
左の図のま出会うまでの距離は3で表しています。右の図は150kmまでを(3+2)で5で表しました。
これを比の式にすると□:4=3:5です。5×□=12 □=12/5 2と2/5時間かかりました。
2/5時間は60分を掛けると24分に変換できます。 答え 2時間24分

3:5にするところが難しいです。図を見れば確かにそうですが何も考えないですると3:2にしてしまいそうです。

そうですね。図解できると誤解がなくなると思います。
4.グラフを使わない速さの問題
*速さ×時間=道のり 道のり÷速さ=時間 道のり÷時間=速さを自由に操れるようにしてください。
〇のついているものを求める場合は・は×、ーは分数の線と覚えましょう。
下図のようにすることで公式が覚えやすくなります。求めるものに対して単に丸を付けるだけなので便利です。

練習問題
AB間20kmを時速8kmの小舟で往復します。川の流れは時速4kmです。
➀流れがない場合AB間にかかる時間を求めましょう。
➁上りにかかる時間は何時間ですか。
③下りにかかる時間は何時間ですか。
④往復の平均の速さを求めなさい。
5.解答
①道のり÷速さ=時間を使いました。 20÷8=2.5 答え2.5時間または2時間30分
ここで時間を分に直す場合と分を時間に直す場合を確認しておきましょう。
- 時間を分に直す場合:小数、または分数に60をかける。1時間は60分だからです。
- 分を時間に直す場合:60で割る。割り切れないときは分数で表します。
②上りは流れに逆らって進みますので小舟は進みが遅くなります。 よって8-4=4kmの速さになります。20÷4=5 答え5時間
③下りは流れに乗りますから小舟は進みが速くなります。 よって8+4=12kmの速さになります。 20÷12=5/3 答えは1時間40分
- 5/3時間に60をかけて100分になりました。それを時間に直したものが1時間40分です。
もう一つの考え方があります。
それは船の進む速さに着目することです。上りの速さは時速4kmで下りの速さは時速12kmになりました。速さは3倍ですね。すると時間は3分の1になります。いわゆる反比例の関係です。
したがって、上りは5時間でしたので3分の1をかければ良いことがわかりました。
④往復の道のりは40km、かかった時間は6時間40分です。
平均という言葉に惑わされないでください。往復の道のり÷往復にかかった時間=平均の速さですから40÷20/3=6 答え 時速6km
*20/3(3分の20)は6と60分の40を仮分数にして約分したものです。